Aatom, molekul, kristall

1 Aatomi siseehitus, kvantfüüsika

Autor: Henn Käämbre

1998. aastal kirjastuses Koolibri ilmunud füüsika õpiku veebiversioon.

Kaane kujundanud Toomas Pääsuke

Joonised Toomas Pääsuke, Alari Savelli, Nils Austa

Toimetaja Enn Randma

1.1 Sissejuhatuseks

Mikros on kreeka keeli väike ja makros suur.

Eesliiteid mikro- ja makro- tarvitatakse üsna erinevais tähendustes. Lepime kokku, et selles raamatus mõistame mikromaailma all aatomite ja molekulide ning nende koostisosade - elektronide, prootonite, neutronite jt aine algosakeste (elementaarosakeste) maailma. Mikrofüüsika hõlmab mikromaailmas valitsevaid seadusi ja seaduspärasusi. Sõnaga makromaailm tähistame seevastu seda, mida vahetult pakuvad meile meie aistingud ja tajud, olgu ka teravdatud ning täiustatud mikroskoobi ning teleskoobi abil. Makrofüüsika on siis makromaailma füüsika. Makrofüüsikat nimetatakse tihti ka klassikaliseks füüsikakas, sest tema alused on rajatud juba 17. sajandil. Peagi näeme, milliseid üllatusi, veidrana ja uskumatuna näivat pakub mikrofüüsika makrofüüsikaga võrreldes. Mikrofüüsika on tekkinud ja arenenud meie sajandil, 20. sajandil. Eeldused tema tekkeks kujunesid sajandivahetuse aastail, siis kui avastati elektron, röntgenikiired, radioaktiivsus, aatomituum.

Mikrofüüsikas õpime tundma aine pisimaid algehituskive ja seda, kuidas neist koostuvad nähtavad ja kombitavad kehad, kõik aistitav, kõik see, millega tegeleb makrofüüsika. Kummatigi on makrofüüsika vundamendiks, millele rajaneb ka mikrofüüsika. Üksnes oma vahetust kogemusest ja katsest võime ammutada juhtmõtteid ja ideid, et hoomata seda, mis toimub meist miljardeid kordi väiksemate objektide maailmas. Mikrofüüsikat on küll palju raskem mõista, uurida ja õppida kui klassikalist. Kuid selle raskuse korvab kuhjaga rahuldustunne, mida võime kogeda, kui oma mõistuse ja teravmeelsete kaudkatsete varal jõuame selle adumiseni, milleni küündimine võib esmapilgul lausa võimatuna tunduda. Mikrofüüsika on ehe kaasaja füüsika.

1.2 Aatomi planetaarmudel

Siin saame teada

Kuidas tekkis vist kõige tuntum aatomite mudel - planetaarmudel?
Kas planetaarmudel kirjeldab reaalsust hästi?

1.2.1 Aatom kui pisike Päikesesüsteem

Nüüdisinimesele on harjumuspärane ja tuttav aatomi planetaarmudel. Seda võib tihti kohata aimeraamatuis, plakateil, logodes. Ta on saanud aatomiajastu sümboliks.

Planetaarmudel sai alguse aatomituuma avastamisest 1911. a. Kui Inglise suurfüüsiku Ernest Rutherfordi õpilased Hans Geiger (1882-1945) ja Ernest Marsden (1889-1970) kiiritasid kullalehekest raadiumikübemest kiirguvate $α$ -osakestega, avastasid nad ootamatult, et mõned osakesed põrkusid kulla-aatomeilt, üksikud koguni tagasisuunas. (Nende katset on lähemalt kirjeldatud näiteks J.Lõhmuse õpikus.)

Rutherfordi arvutused näitasid, et see olnuks mõeldamatu, kui aatomi positiivne elektrilaeng jaotuks ühtlaselt üle aatomi ruumala. Et aga aatom on tervikuna neutraalne, peab ta sisaldama elektronide negatiivse laenguga võrdset positiivset laengut. Ainuvõimalik seletus oli, et positiivne laeng on koondunud elektronidest tuhandeid kordi massiivsemasse kompaktsesse tuuma.


Ernest Rutherford (1871–1937) oma sünnimaa Uus-Meremaa kirjamargil	Hans Geiger (1882–1945)

Planetaarmudeli järgi sarnaneb aatom pisitillukese (umb. $10^{23}$ – sada tuhat miljardit miljardit korda vähendatud) Päikesesüsteemiga. “Päikeseks” on aatomituum, “planeetideks” tuuma ümber tiirlevad elektronid. Mitmesuguste katsetega on välja uuritud, et aatomi mõõtmed on suurusjärgus $10^{- 10} m$ ( $= 10^{- 8} c m$ ), tuuma omad – $10^{- 15} m$ ( $= 10^{- 13} c m$ ). Teadlased on otsusele jõudnud, et elektroni mõõtmeid polegi võimalik hinnata, teda käsitatakse punktmassina. Tuumad koosnevad positiivse laenguga prootonitest ja laenguta, neutraalseist neutronitest. Ainult lihtsaima aatomi, vesinikuaatomi tuumaks on üksainus prooton. Absoluutväärtuselt on prootoni laeng täpselt võrdne elektroni laenguga ( $1, 6 \cdot 10^{- 19} C$ ). See on elementaarlaeng. Prooton ja neutron on ligilähedalt võrdse massiga, mis umb. $2000$ korda ületab elektroni massi. (Täpsed arvandmed on tabelis raamatu lõpus.) Et aatom tavaolekus on laenguta, peab prootonite arv tuumas ja teda ümbritsevate elektronide arv olema võrdne. See on laenguarv Z – aatomi tähtsaim iseloomustaja.

Tavaliselt joonistatavad planetaarmudeli skeemid, nagu ülaltoodugi ei anna õiget ettekujutust tegelikest suurusvahekordadest. Et neist aimu saada, võiks kujutleda aatomit jalgpalliväljaku suurusena, tuum selle keskel oleks siis umbes nööpnõelapea mõõtmetega. (Kujutledes samasuurt Päikese-süsteemi mudelit, oleks Päike selles nagu pähkel). Seega on aatom peaaegu “täiesti tühi”: tuumaaines hõlvab koguruumalast sajatuhandendikosa. Seepärast põrkasidki α-osakesed kullakilelt tagasi haruharva – ainult siis, kui tabasid otse tuuma. Ometi on just tuumasse koondunud peaaegu kogu aatomi mass.

Järelemõtlikumad õppurid võivad küsida siin: miks on siis nõnda tühjadest süsinikuaatomeist koosnev teemant nii kõva, või miks paljud ained ei lase oma tühjusest hoolimata valgust läbi? Vastuse püüame anda edaspidi, kui oleme aatomi ehitusega lähemalt tutvunud.

1.2.2 Planetaarmudeli vastuolud

Joon. 2.3 Kui elektron järgiks makrofüüsika seadusi...

Päikesesüsteemi hoiavad koos gravitatsioonijõud, planetaaraatomit elektrilised tõmbejõud positiivse tuuma ja negatiivsete elektronide vahel. Mikroosakeste vahel mõjuvad gravitatsioonijõud on kaduvväikesed ega mängi mingit rolli. Elektrikursuses saab arvutada, et et elektriline jõud on vesinikuaatomis gravitatsioonijõust umbes $10^{39}$ korda suurem.

Päikesesüsteem on peaaegu muutumatuna püsinud juba aasta-miljardeid. Nõnda püsiv saab ta olla vaid alalises liikumises (sõna planeetki tähendab kreeka keeles rändajat, ekslejat). Kui planeedid oleksid paigal, tõmbaks Päikese ja planeetide vaheline gravitatsioonijõud nad Päikesele ja süsteem oleks ammugi hukkunud. Kuid (meile õnneks!) on planeetidel ka orbiidi puutuja suunaline kiirus (tangentsiaalkiirus). Päikesele langemise asemel nad justkui kukuvad sellest kogu aeg mööda. Gravitatsioonijõud omandab tiirleva planeedi jaoks kesktõmbejõu ehk tsentripetaaljõu rolli (vrd. joon. 2.2). Täpselt samuti võiks oletada, et elektronide tiirlemine aatomis teebki aatomi püsivaks. Sellest planetaarmudel lähtubki.

Paraku ilmneb siin üks ülesaamatu raskus, mida võiks piltlikult nimetada planetaarmudeli kiirgamistõveks. Elektrifüüsikast on teada, et võnkuvad elektrilaengud kiirgavad alatasa elektromagnetlaineid, samuti kui veepinda puudutav võnkur loksutab vee lainetama. Kuid tiirlemist võib kujutleda teineteisega risti olevate võnkumiste summana. (Vaata näit. nööri otsas tiirutatavat palli tiirlemistasandis: pall näib võnkuvat.) Siis peaks ka tiirlevad elektronid kogu aeg elektromagnetlaineid kiirgama. Elektromagnetlained kannavad ära energiat ja energia jäävuse seaduse järgi peab siis tiirleva elektroni energia alatasa vähenema. Ühtlasi väheneb elektroni orbiidi raadius, kuni ta lõpuks langeb spiraali mööda tuumale ja aatomit polegi enam. Arvutuste järgi peaks see juhtuma ülikiiresti, umbes $10^{- 9}$ sekundi jooksul, miljardeid kordi lühema ajaga kui kulub trükirea lugemiseks. Stabiilsuse asemel saime hoopis katastroofilise ebastabiilsuse! Võrdluseks: midagi taolist juhtub ka maalähedastele orbiitidele lennutatud sputnikutega – nemadki kaotavad õhkkonna takistust ületades energiat ja spiraalivad lõpuks atmosfääri tihedatesse alakihtidesse, kus lõpuks ära põlevad.

1.2.3 Aatomite püsikindlus

Teame hästi, et tegelikkuses ei toimu aatomitega midagi niisugust. Vastupidi, aatomid on väga püsivad moodustised. Näiteks võime aatomeid ioniseerida, mõjutades neid ultravalgusega või tugeva elektriväljaga. Niiviisi lööme neilt elektrone välja, lõhume neid. Kuid niipea kui ioniseeritud aatom haarab “röövitute” asemele uued elektronid, taastub ta täpselt endisena. Edasi, kaks sama elemendi aatomit on üksteisega eristamatult sarnased. Ei saa nt vahet teha maailmaruumist raudmeteoriidiga saabunud raua-aatomi ja maapealsest kaevandusest toodetud raua aatomi vahel. Element heelium avastatigi tema spektri kaudu esmalt Päikesel (Helios - kr. k. Päike), alles siis leiti teda ka Maal. Aatomite “standardiseeritus” on ülirange.

Järeldus saab olla ainult üks: mikroosakeste maailmas, aatomimaailmas toimivad mingid uudsed seaduspärasused, mis on sootuks erinevad neist, mida tunneme makrofüüsikast, meie endiga lähedaste mõõtmetega või ka meist palju suuremate objektide maailmast. Neid seaduspärasusi tulebki meil nüüd otsima asuda. Mis võiks meile teed näidata? Kust võiksime saada aatomite kohta lisateavet, mis aitaks lahti sõlmida nende müsteeriumi? Üheks põhiliseks infokandjaks meile on valgus. Nägemise kaudu saame teada umbes $4 / 5$ meie ümber toimuvast. Valgus toob meile teateid kaugest maailmaruumist, ehk siis ka aatomimaailma sügavustest. Tuleb vaid õppida neid teateid lugema.

Stopp! Jäta meelde!

Aatomituuma olemasolu

Aatomituuma olemasolu näitas $α$ -osakeste hajumine aatomeilt.

Aatomi läbimõõt

Aatomi läbimõõt on suurusjärgus $10^{- 10} m$ , tuuma läbimõõt - $10^{- 15} m$ .

Aatomi planetaarmudel

Aatomi planetaarmudel kujutab aatomit miniatuurse Päikesesüsteemina, milles elektronid tiirlevad ümber tuuma nagu planeedid ümber Päikese.

Aatomi planetaarmudeli ebatäiuslikkus

Planetaarmudel ei seleta aatomite püsivust ega sama elemendi aatomite täpset sarnasust ning taastatavust: tiirlevad elektronid peaksid makrofüüsika seaduste järgi pidevalt kiirgama elektromagnetlaineid ja niiviisi energiat kaotades langema $10^{- 9} s$ jooksul tuumale

Aatomite püsikindlus

Aatomite püsikindluse seletamiseks tuleb otsida mikroosakeste omadusi, mis neid järsult eristavad makrokehadest.

Küsimused ja ülesanded

Mis liiki jõud põhjustasid

α

-osakeste hajumist Rutherfordi uurimiskaaslaste katsetes?

answer

Kas elektroni kiirus planetaarmudeli orbiidil suureneb või väheneb, kui elektron kulutab kiirgamiseks energiat?

answer

Mille poolest erineb tehiskaaslase Maale langemine ja häving planetaarmudeli elektroni tuumale langemisest?

answer

Lisamaterjalid Lisaülesanded

1.3 Spektrijooned kui redel aatomimaailma

Siin saame teada

Kuidas on aatomite siseehitus seotud aatomite kiiratava valguse spektriga.
Kuidas on aatomite kiirgus- ja neeldumisspektrid seotud aatomite omadustega.

1.3.1 Aatomite spektrijooned ja energiatasemed

Optikakursuses õppisime, et kui hõrendatud gaasidest elektrivoolu läbi juhtida, kiirgavad need valgust, mille spekter on joonspekter. Teisisõnu, nende helendus ei sisalda igasuguse lainepikkusega valgust, vaid liitub teatavate kindlate lainepikkustega valgusvoogudest. Hõrendatud gaasides (nt elektrilahenduses läbi vesiniku, neooni, naatriumiauru jne) kiirgavad üksteist vähe mõjutavad üksikaatomid. Niisiis, joonspektrid on aatomite spektrid.

Kindlad lainepikkused tähendavad ka kindlaid sagedusi, sest sagedus

f = \frac{c}{λ}

kus $c$ on valguse kiirus vaakumis ja $λ$ lainepikkus. Kui meenutame valguse kaksisust (dualismi), taipame, et joonspekter tähendab ühtlasi seda, et aatomeist kiiratakse kindla energiaga footoneid. On ju footoni energia

E = h f

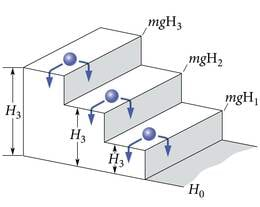
( $h$ on Plancki konstant). Kindla energiaga footonit kiirates peab aatom kaotama footoni energiaga $E$ võrdse energiaportsjoni (energia on jääv!). Samaviisi kaotab trepil astmelt astmele veerev kuulike (joon. 3.1) oma potentsiaalset energiat $m g H$ Maa raskusväljas hüpete $Δ E_{1} = m g (H_{3} - H_{2})$ , $Δ E_{2} = m g (H_{2} - H_{1})$ , $Δ E_{3} = m g (H_{1} - H_{0})$ kaupa. Siin on $m$ – kuulikese mass, $g$ – raskuskiirendus, $H$ – astme kõrgus; $H$ , et seda ei aetaks segi Plancki konstandiga $h$ .

Δ E = m g H_{i} - m g H_{j}

See hüppelisus viib mõttele, et aatomiski on elektronid kindlail energiatasemeil, mis püsivalt omased igale aatomiliigile (elemendile). (Meenutame spektraalanalüüsi – aatomite “sõrmejälgi”.) Nõndasamuti saame meiegi seista vaid redeli pulkadel, mitte nende vahel. Elektroni langedes kõrgemalt (suurema energiaga) tasemelt madalamale, kiiratakse valguskvant energiaga

h f = E_{k} - E_{m}

kus $E_{k}$ ja $E_{m}$ on vastavalt kõrgema ja madalama taseme energia.

Siinkohal tuleks märkida, et aatomifüüsikas mõõdetakse energiat sageli süsteemivälistes ühikutes – elektronvoltides. Neis ühikuis väljenduvad mikromaailma energiakvantumid lühikeste, ülevaatlike arvudena.

Elektronvolt

$1$ elektronvolt ( $e V$ ) on energia, mille omandab elektron, läbides elektriväljas potentsiaalide vahet $1$ volt. $1 e V = 1, 60 \cdot 10^{- 19} J$ .

Joon. 3.2. Sageduste kombineerumine spektris.

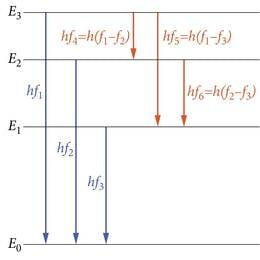
Analüüsides erinevate gaaside spektrijoonte paiknemist sagedusskaalal, leiame veelgi kinnitust kujutlusele energiatasemeist. Nimelt, kui spektris esinevad jooned sagedustel $f_{1}$ , $f_{2}$ , $f_{3}$ jne, siis leiduvad samas spektris arutihti ka jooned, millele vastab sagedus $f_{4} = f_{1} - f_{2}$ , $f_{5} = f_{1} - f_{3}$ , $f_{6} = f_{2} - f_{3}$ . (sageduste kombinatsiooniprintsiip, tihti nimetatud ka tema märkaja, Šveitsi füüsiku Walter Ritzi (1878 - 1909) järgi Ritzi kombinatsiooniprintsiibiks).

Silmitsedes joonist 3.2, leiame, et kõik kombinatsioonid saavad lihtsa seletuse, kui footoneid kiiratakse elektroni “hüpetel” tasemelt $E_{3}$ tasemele $E_{0}$ , $E_{2} \to E_{0}$ jne., nii et $h f_{1} = E_{3} - E_{0}$ , $h f_{2} = E_{2} - E_{0}$ , $h f_{3} = E_{1} - E_{0}$ , $h f_{4} = E_{3} - E_{2}$ jne.

1.3.2 Allakäigutrepilt üles

Joon. 3.3. Vesiniku aatomi kiirgusspekter (A) ja neeldumisspekter (B) nähtavas spektriosas; skaala ühikuis 10^-8m (pügalad 50 nm kaupa).

Et kuulike saaks trepiastmeilt alla veereda, tuleb ta enne üles viia. Aatomi ja elektronide puhul ütleme: aatomit tuleb ergastada, talle energiat sisestada, et tal oleks, mida välja kiirata. Seda võib teha väga mitmel viisil, nt kiiritades aatomeid sobiva spektraalkoostisega valgusega või elektronkimbuga, ainet kuumutades jne. Kas aatomi elektronide energiatasemed avalduvad ka ergastamisel?

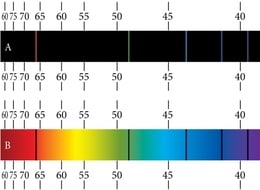
Meenutame optikast neeldumisspektreid, mis saadakse, kui pideva spektriga valgusallika valgus läbib nt. gaasi või auru. Tumedad neeldumisjooned neeldumisspektris langevad täpselt kokku heledate joontega kiirgusspektris (joon. 3.3). See näitabki, et aatomid saavad energiat ka vastu võtta üksnes kindlate portsjonite kaupa. Neelatavad energiakvantumid peavad vastama energiatasemete vahedele.

Franck-Hertzi katse

Aga mis siis, kui energiat ei loovuta footonid, vaid aatomitega põrkuvad elektronid? Sellele küsimusele saab vastust otsida joon. 3.4 visandatud katseriista abil.


Joon. 3.4 Francki ja Hertzi katseseade.	Francki ja Hertzi katse tulemus.

Klaasballooni $B$ on joodetud 3 elektroodi: hõõgkatood $K$ , võre $V$ ja anood $A$ . Toru $T$ kaudu saab ballooni õhust tühjaks pumbata ja täita mitmesuguste gaaside või aurudega. Hõõgkatood kiirgab elektrone, mida kiirendatakse võrele antud positiivse pinge $U_{K V}$ ajel. Pinget $U_{K V}$ saab sujuvalt muuta ( $0...30 V$ ). Elektroodide $V$ ja $A$ vahele on rakendatud nõrk ( $\sim 0, 5 V$ ) vastupinge $U_{V A}$ , mis võret läbinud elektrone pisut aeglustab.

Tõstame pinget $U_{K V}$ ja mõõdame anoodile $A$ jõudvate elektronide voolu $I_{K A}$ pikoampermeetriga $p A$ . Kui balloonis on vaakum, kasvab vool sujuvalt (punktiir graafikul). Laseme ballooni pisut naatriumiauru (rõhuni umb. $1 / 1000$ atmosfäärirõhust) ja kordame katset. Vool kasvab nüüd hoopis keerukamalt, perioodiliselt korduvate hüpetena. Kui esimene langus ilmub pingel $U_{1}$ , siis järgmine pingel $2 U_{1}$ , edasi $3 U_{1}$ jne. Pinge jõudes $U_{1}$ -ni ilmub ballooni $N a$ kollane helendus.

Mis toimub? Kui elektronide energia on väiksem kui $E_{1} = e U_{1}$ , ei kaota nad energiat põrgetel $N a$ -aatomitega, suudavad ületada vastupinget $U_{V A}$ ja jõuavad anoodile. Kuid pingel $U_{1}$ saavutatakse energia, mida $N a$ -aatomid saavad elektronidelt põrgetel omastada. Aatomid ergastuvad ja hakkavad helenduma. Energiat kaotanud elektronid ei suuda enam ületada vastupinge “astangut”, pöörduvad võrele tagasi ja vool langeb järsult. Langused $2 U_{1}$ , $3 U_{1}$ jne juures näitavad, et elektronid on saanud elektriväljalt piisavalt energiat $2$ , $3$ jne aatomi ergastamiseks.

Kriitiliste pingete väärtused sõltuvad ballooni täitvast gaasist/aurust: naatriumi puhul on $U_{1} \sim 2, 1 V$ , elavhõbeda aurus $\sim 4, 9 V$ , vesinikus $\sim 10, 2 V$ , heeliumis $20, 6 V$ . Energiad $E_{1} = e U_{1}$ on võrdsed kiirguvate footonite energiatega.

Neist katseist järeldub, et mitte ainult footonid, vaid ka mikroosakesed saavad loovutada aatomeile energiat ainult kindlate kvantumite viisi.

Seda katset tuntakse esmasooritajate, Saksa füüsikute James Francki (1882-1964) ja Gustav Hertzi (1887-1975) järgi Francki ja Hertzi katsena (1914).

1.3.3 Seaduspära vesiniku aatomi spektris

Joon. 3.5. Vesiniku spektrijoonte seeriad:
A – laias spektriosas ultravalgusest infravalguseni,
B – Balmeri seeria (osalt nähtav) spektrifoto (vrdl ka joon. 3.3)

Meil on nüüd küllaldaselt tõendusmaterjali, et iga elemendi aatom võib asuda ainult talle omastel energiatasemetel. Energiat võtab ja annab aatom üksnes kindlate kvantumitena, mis võrduvad mingi kahe taseme energia vahega. Jääb küsimus, miks need tasemed kujunevad. Vihje vastuse leidmiseks annavad taas spektrid.

Võtame vaatluse alla lihtsaima, vesiniku aatomi spektri (joon. 3.5). Tundmatusse tungimist tuleb ikka alustada võimalikult lihtsast erijuhust, et vältida hägustavaid keerukusi, mis segavad tabamast peamist, põhilist.

Märkame seaduspära spektrijoonte asendeis: jooned on rühmitunud spektraalseeriatesse, igas seerias moodustavad jooned koonduvaid jadasid. Täppisanalüüs näitab, et kõiki seeriajadasid kirjeldab valem

(3.1)

\frac{1}{λ} = R (\frac{1}{n_{1}^{2}} - \frac{1}{n_{2}^{2}})

kus $λ$ on joone lainepikkus, $R = 1, 0974 \times 10^{7} m^{- 1}$ on Rydbergi konstant, ning $n_{1}$ ja $n_{2}$ on täisarvud: $n_{1}$ on igas seerias konstantne täisarv (vt. tabel) ja $n_{2} = n_{1} + 1, n_{1} + 2, n_{1} + 3 . . .$ .

Valemi (3.1 ) koostas juba 1885 lihtsalt proovimismeetodil Šveitsi gümnaasiumiõpetaja Johann Balmer (1825–1898), siintoodud ülevaatliku ja lihtsa kuju andis Balmeri valemile rootslane Johannes Rydberg (1854–1919), tema nimest ka konstant $R$ .

Vesiniku spektraalseeriad

Seeria nimi avastaja järgi (sulgudes avastamisaasta)	$n_{1}$	$n_{2}$
Lymani seeria (1906)	$1$	$2, 3, 4 . . .$	Ultravalgus ( $91, 2 - 121, 6 n m$ )
Balmeri seeria (1885)	$2$	$3, 4, 5 . . .$	Nähtav valgus ( $364, 7 - 656, 5 n m$ )
Pascheni seeria (1908)	$3$	$4, 5, 6 . . .$	Infravalgus ( $820, 1 - 1875, 6 n m$ )
Bracketti seeria (1922)	$4$	$5, 6, 7 . . .$	Infravalgus ( $1458, 8 - 4052, 2 n m$ )
Pfundi seeria (1924)	$5$	$6, 7, 8 . . .$	Infravalgus ( $2279, 4 - 7459, 9 n m$ )

Rõhutasime sõna täisarvud. Kas kohtame lihtsat täisarvulist, diskreetset muutumist ka kusagil makrofüüsikas, kus üldiselt oleme harjunud kõigi suuruste ühtlase, sujuva varieerumisega?

1.3.4 Helisev pillikeel

Joon. 3.6. Mõned võimalikest seisulaineist otstest kinnitatud pinguli traadil (hele triip – traadi paigalasend).

Kui sõrmega või poognaga tõmmates viime pillikeele tasakaaluseisust välja, tekitame keeles laineid. Olenevalt puutekohast ja keele pingsusest, võivad need lained olla väga mitmesuguste pikkustega. Kõik lained on aga sulustatud keele kinnituskohtade vahele. Sulustatud lained teisenevad alati seisulaineteks, milles võnked toimuvad ainult paisudes, paigale jäävate sõlmede vahel. Levides keele kinnitisteni, peegelduvad lained nendelt tagasi. Keelel levivate ja kinnitiselt peegeldunud lainete interferentsist sünnivadki seisulained. Tõusuinterferentsis paisuda saavad ainult kindla pikkusega seisulained, sellised, mille poollaine pikkus mahub täisarv kordi keele pikkusele $L$ (joon. 3.6):

(3.2)

\begin{matrix} 1 \cdot \frac{1}{2} λ_{1} = L 2 \cdot \frac{1}{2} λ_{2} = L 3 \cdot \frac{1}{2} λ_{3} = L \dots n \cdot \frac{1}{2} λ_{n} = L \end{matrix}

Ei saa tekkida seisulained, milles nt. $1, 2 \cdot λ_{1} = L$ : siis peaks ka kinnitatud keeleots võnkuma. Kõik lained, mille pikkus ei rahulda seost (3.2 ), kustuvad kiiresti leviva ja peegeldunud laine mõõnainterferentsil. Pikemalt kestma jäävad üksnes seisulained pikkusega $λ = 2 L / n$ . Nende summa annabki keele helina: pikim, $λ_{1} = 2 L$ tekitab põhitooni, lühemad – ülemtoonid.

Olemegi leidnud täisarvulised suhted ning diskreetse, hüppelise muutumise ka makromaailmast: need ilmuvad seisulainete juures.

Küsimused ja ülesanded

Miks värvub gaasileek kollaseks, kui veepott tulel üle keeb ja veepiisad leeki satuvad?

answer

Miks ilmuvad neeldumisspektrisse tumedad jooned? Kui aatom neelab footoni energiaga

h f = E_{k} - E_{m}

, peaks ta kohe tagasisiirdel ju samasuguse kvandi ka tagasi kiirgama, nii et ainet läbiv valgusvoog ei tohiks üldse nõrgeneda. Teisipidi: miks ei kahane valguse heledus neeldumisjoontes nulliks? (Vihje: footoneid kiiratakse kõikvõimalikes suundades.)

answer

Lühilainelise ultravalguse spektrite uurimiseks tuleb kogu spektraalaparatuur koos uuritava valguse allikaga paigutada vaakumisse. Miks? (Vihje: miks näeme halvasti läbi tumeda klaasi?)

answer

Mis liiki energiaks muundub lõppeks astmelt astmele veereva kuulikese potentsiaalne energia?

answer

Stopp! Jäta meelde!

Aatomite energiatasemed

Aatomite kiirgus- ja neeldumissepektrid on joonspektrid, seega võib aatom energiat omandada ja loovutada ainult kindlate kvantumite viisi.

Spektrijoonte asetus

Spektrijoonte asetuses on täheldatav korrapära.

Vesiniku spektrijooned

Lihtsaima aatomi, vesnikiku aatomi spektrijooned paiknevad koonduvate jadade - spektraalseeriatena. Kõiki seeriaid kirjeldab Balmeri-Rydbergi valem

\frac{1}{λ} = R (\frac{1}{n_{1}^{2}} - \frac{1}{n_{2}^{2}})

Siin $n_{1}$ ja $n_{2}$ on täisarvud. See viitab seosele seisulainetega, mille sõlmede-paisude arv muutub samuti ühekaupa, diskreetselt.

Testi ennast!

Spektrijooned kui redel aatomimaailma: kas sain aru ja oskan kasutada?

Testi tegemiseks on aega 30 minutit. Tulemused ilmuvad kohe ePortfooliosse.

Open

Lisamaterjalid

1.4 Elektron "lainetab"

Siin saame teada

Sarnaselt valgusega on ka osakestel lainelised omadused.
Kuida määrata elektroni lainepikkust
Mida arvata mõttest, et ka liivatera on laine.

1.4.1 Söakas hüpotees

Aatomispektrite korrapära kõrvutamine seisulainetega juhib mõttele, et aatomi energiatasemed ja spektrite seaduspära saaksid seletuse, kui aatom meenutaks seisulainetes võnkuvat viiulikeelt. Spektrid kajastavad elektronide siirdeid energiatasemete vahel. Tähendab, seisulainete olekus peaksid olema elektronid. Selleks peavad elektronid omama laineloomust. Esialgu näib see mõtegi üsna võõrastav. Elektron on ju osake! Tema liikumisteed saab jälgida Wilsoni udukambris või mullikambris – vt. joon. 4.4 (neist katseriistust loeme lähemalt tuumafüüsika osast), teda saab elektri- ja magnetväljade abill kallutada ostsillograafi ekraani eri punktidesse, tal on muutmatult kindel seisumass. Osake on meie tavamaailmas kujunenud kujutluse, “terve mõistuse” järgi midagi sootuks erinevat lainest.

Kuid tuletame meelde kvantoptikat: valguslained võisid teatud olukordades käituda kui osakeste, footonite voog. Looduses kohtame tihti sümmeetriat: on positiivsed ja negatiivsed laengud, osakesed ja antiosakesed, sümmeetrilised on kristallid, kasvõi lumehelbed... Ons siis nii uskumatu sellinegi sümmeetria, et kui on

L A I N E D \to O S A K E S E D

kas ei või siis olla ka vastupidi

O S A K E S E D \to L A I N E D

Sellise hüpoteesi püstitas 1924. a. oma doktoritöös tollal noor ja söakas Prantsuse füüsik, markii Louis de Broglie (loe: lui döbroji). Tolleaegses füüsikkonnas põhjustas see “hull” oletus hämmingut ja õlakehitusi.

Valguse laineloomus selgus interferentsi- ja difraktsiooninähtustest. Ei saa ju ülilühikesi valguslaineid vaadelda otseselt, nagu laineid tiigipinnal või tuules voogaval lipul. Valguslainete olemasolu tõendavad nähtavad vöödid, mis tekivad interferentsikatseis ühtuvate laineharjade ja -nõgude vastastikuse kustutamise ja laineharjade liitumise tulemusena. Kõige otsesemalt tõlgendatav on interferentsikatse, mille korraldas Thomas Young 1801, suunates valgusvihu juuspeenele kaksikpilule.

1.4.2 Elektronlained on olemas!

Kui mikroosakestega tõepoolest seonduvad mingid lained, peaksid needki ilmnema interferentsis ja difraktsioonis. Nii see tõepoolest ongi. Joonisel 4.1 näeme difraktsioonipilti, mille annab alumiiniumi mikrokristalli õhukest kihti läbinud elektronkimp luminestseerival ekraanil või fotoplaadil. Võrdluseks on see kõrvutatud valguse (röntgenkiirguse) difraktsioonipildiga samast eksperimendist. Sarnasus on silmnähtav. Järelikult on elektronilained tõepoolest olemas.

Joon. 4.1. Röntgenkiirte (valguslainete, paremal) ja elektronide (ainelainete, vasakul) hajumine alumiiniumi mikrokristallide õhukeselt kihilt. Pange tähele, et mõlemad pildid langevad geomeetriliselt kokku.

Joon. 4.2. Röntgenkiirte (vasakul) ja elektronide difraktsioonipildid keedusoola monokristallil.

Kui elektronilained muunduvad seisulaineiks aatomis, peavad nad olema väga lühikesed, aatomi mõõtmetele ( $10^{- 8} c m$ ) lähedase pikkusega. Selliste lainete interferentsi ilmutamine on tehniliselt muidugi keerukas. Young oskas valguse kaksikpilukatse teha möödunud sajandi alguse primitiivsete vahenditega, mõningate pingutustega võib seda igaüks korrata. Seevastu elektronide kaksikpilukatse sai võimalikuks hiljuti, kaasaegse elektronmikroskoopia võtteid kaasates.

Kui ilmub interferents, peab olema ka difraktsioon – tõkete taha paindunud lainete interferents. Elektronilained avastatigi esmalt difraktsioonikatsetes. Sobivaiks, vajalikult väikese võrekonstandiga difraktsioonivõredeks osutusid kristallid. Joon. 4.2 on difraktsioonipilt, mille annab soolakristalli läbinud elektronkimp. Võrdluseks on kõrval ülilühikeste elektromagnetlainete – röntgenikiirte difraktsioonipilt. Elektronide difraktsiooni avastasid juhuslikult, tänu katse käigus juhtunud äpardusele (vaakumseadme lekk) 1927. a. USA füüsikud Joseph Davisson (1881–1958) ja Lester Germer (1896–1971) ning nendega pea ühtaegu inglane George Thomson (1892–1975). Märgime seika, et elektroni-osakese avastas 1897 sir Joseph John Thomson (1856–1940), tema poeg George tuvastas sama osakese laineomadused.

1.4.3 Mis lainetab elektronlaines?

Joon. 4.3. Üksikelektronide interferentsipildi kujunemine kaksikpilult; vasakul – elektronide tabamuste ligikaudne arv.

Lainetamine on millegi perioodiline muutumine ajas ja ruumis. Veelaines lainetab veepind, helilaines keskkonna tihedus, valguslaines elektromagnetväli. Aga mis lainetab elektronilaines? Vastuse jälile juhatab meid teisendatud kaksikpilukatse. Selles vähendati elektronkimbu tihedust niivõrd, et elektronid läbivad pilu ühekaupa (vähendades sedavõrd elektrone kiirgava hõõgkatoodi temperatuuri). Katse tulemuseks on joonisel 4.3 esitatud fotojada. Järjestikustel kaadritel näeme järjest suurema arvu üksikelektronide tabamustäpikesi tajur-plaadil (põhimõtteliselt võib selleks olla fotoplaat, kuid nüüdsetes ülitundlikes seadistes kasutatakse tiheda võrguna paigutatud pisikesi elektrilisi andureid).

Mida võime neist piltidest välja lugeda?

See, et iga tabamus annab täpikese, näitab, et elektron ei moondu laineks, vaid jääb ikkagi osakeseks, mis langeb mingisse plaadipunkti.
Kuna esialgu, väikese registreeritud elektronide arvu juures, paiknevad täpikesed korrapäratult, järeldame, et elektronilaine ei määra iga üksikelektroni liikumist rangelt.
Mida rohkem tabamusi, seda selgemalt rühmituvad täpikesed interferentstriipudesse. Et elektronid väljastati ühekaupa, pidi iga üksikelektroniga kaasnev laine pilusid läbinult interfereeruma iseendaga. Kõrvale jääb kahtlus, et elektronid rühmitusid mingi omavahelise vastastikmõju ajel.

Lainetaoline käitumine koorub välja ainult suure hulga elektronide tabamussagedustest tajurplaadi pinna erinevais punktides. Jaotame “märklaua” pinna väikesteks ruudukesteks, loendame igasse ruutu langenud tabamuste arvu $N_{i}$ ja tabamuste koguarvu $Σ N_{i} = N$ . Arvutades suhted $N_{i} / N$ , saame elektroni tabamuse tõenäosuse igasse ruutu. Seega on elektroniga (ja iga mikroosakesega) kaasnevad lained tõenäosuslained. Erinevalt veelainetest, helilainetest jne, pole nad lained mingis materiaalses keskkonnas.

Füüsikud nimetavad nende lainete konkreetset kuju ja ajalist muutumist kirjeldavat matemaatilist avaldist lainefunktsiooniks. On tavaks tähistada seda funktsiooni kreeka psii-tähega $Ψ$ . Vahel öeldaksegi lihtsalt psii-funktsioon. Suuruse $Ψ$ väärtus ruumipunktis koordinaatidega $x, y, z$ hetkel $t$ , $Ψ (x, y, z, t)$ määrab osakese leiutõenäosuse antud kohal ja ajal. Kuid laines võib hälve olla nii positiivne (tasakaaluasendist üles) kui negatiivne (tasakaaluasendist alla).

Negatiivsel tõenäosusel pole aga mõtet. Kui aga võtame hälbe ruutu, $Ψ \to Ψ^{2}$ , saame alati positiivse suuruse. See siis annabki tegelikult leiutõenäosuse:

Osakese leidmise tõenäosus antud punktis ja hetkel

Leiulaine hälbe ruut $Ψ^{2}$ on võrdeline osakese leiutõenäosusega antud punktis ja hetkel.

(Meenutame, et analoogiliselt mõõdab optikas valguse intensiivsust valguslaine elektrivektori ruudu keskväärtus).

Nimetus lainefunktsioon pole eriti õnnestunud, sest samahästi võiks nõnda nimetada mistahes laineid kirjeldavat funktsiooni. Seepärast nimetame järgnevas mikroosakeste leiutõenäosust määravaid laineid lühidalt leiulaineteks.

Tõenäosuslikkus mikroosakese käitumises pole tingitud meie mõõtmisoskuste või -aparaatide puudulikkusest ega objektide suurest hulgast. Ta on olemuslikult, sisemiselt omane mikroosakestele nagu elektron, prooton või neutron.

Elektronilaineid hakkas tõlgendama leiutõenäosuse lainetena juudi rahvusest Saksa füüsik Max Born. Nüüdisfüüsikas on see tõlgendusviis üldtunnustatud.

1.4.4 Elektroni lainepikkus

Laineid iseloomustab lainepikkus $λ$ . Kuidas määrata elektroni leiulaine pikkust?

Optikas arvutasime footoni massi, rakendades relatiivsusteooriast tulenevat üldkehtivat seost energia $E$ ja massi $m$ vahel:

E = m c^{2}

Teiselt poolt, footoni energia $E = h f$ , kus h on Plancki konstant ja $f$ valguse võnkesagedus. Seega

m c^{2} = h f

ehk

m = \frac{h f}{c^{2}}

Kuna $f = c / λ$ , siis

m = \frac{h c}{c^{2} λ} = \frac{h}{c λ}

Siit

λ = \frac{h}{m c}

Footoni massi ja kiiruse korrutis $m c$ on tema impulss $p$ . Niisiis

λ = \frac{h}{p}

Oletame, et sama seos kehtib ka seisumassiga osakeste, sh. elektroni kohta. Siis on impulss $p = m v$ , kus $v$ on osakese kiirus, ja

(4.1)

λ = \frac{h}{p} = \frac{h}{m v}

See de Broglie’ tuletatud valem on üks olulisemaid mikrofüüsikas. Valemist (4.1 ) määratud lainepikkust nimetatakse ka de Broglie’ lainepikkuseks ning vabalt liikuvate osakeste leiulaineid – de Broglie’ laineteks.

Näidisülesanne 1-1

Leida elektrivälja potentsiaalide vahet $100 V$ läbinud elektroni leiulaine pikkus.

Lahendus

Andmed

$U = 100 V$
$m = 9, 1 \cdot 10^{- 31} kg$
$h = 6, 6 \cdot 10^{- 34} J \cdot s - ------------------- -$
$λ - ?$

Arvutused

Lainepikkuse leiame de Broglie’ valemist

λ = \frac{h}{p}

Elektroni impulsi $p$ arvutame tema kineetilise energia $E_{k}$ kaudu. Et

E_{k} = \frac{m v^{2}}{2} = \frac{p^{2}}{2 m}

siis

p = \sqrt{2 m E_{k}}

λ = \frac{h}{\sqrt{2 m E_{k}}}

Läbinud väljapinge $U$ volti, saab elektron kineetilise energia $U$ elektronvolti, kusjuures teame, et $1 e V = 1, 60 \cdot 10^{- 19} J$ , seega

E_{k} = 100 e V = 1, 6 \cdot 10^{- 17} J

Nii et

λ = \frac{6, 6 \cdot 10^{- 34} J \cdot s}{\sqrt{2 \cdot 9, 1 \cdot 10^{- 31} k g \cdot 1, 6 \cdot 10^{- 17} J}} = 1, 22 \cdot 10^{- 10} m \sim 0, 12 n m - ------- - - ------- -

Vastus. $100$ -voldise pingega kiirendatud elektronide lainepikkus $λ = 1, 2 \cdot 10^{- 10} m = 0, 12 n m$ . Tegemist on röntgenkiirgusega. Õppuri kontrollida jäägu, et

\frac{J \cdot s}{\sqrt{k g \cdot J}} = m

Näidisülesanne 1-2

Millise lainepikkusega ( $λ_{e}$ ) elektronid tekitavad röntgenkiirguse, mille lühim lainepikkus $λ_{r}$ on $0, 05 nm$ ?

Lahendus

Andmed

$λ_{r} = 0, 05 μ m = 5 \cdot 10^{- 11} m$
$h = 6, 6 \cdot 10^{- 34} J \cdot s$
$m = 9, 1 \cdot 10^{- 31} k g$
$c = 3 \cdot 10^{8} m / s - -------------- -$
$λ_{e} - ?$

Arvutused

Röntgentorus kiirendatakse hõõgkatoodist kiirguvaid elektrone kõrgpingeväljas. Põrkudes vastu anoodi, elektronid aeglustuvad järsult ja nende kineetiline energia muundub röntgenkiirguse footonite energiaks: laengute kiirendatud liikumisel (aeglustus on negatiivne kiirendus!) tekib alati elektromagnetkiirgus, röntgenkiirgus ongi väga lühilaineline elektromagnetkiirgus.

Energia jäävuse tõttu ei saa suurima energiaga (kõige lühilainelisemate) röntgenkiirguse footonite energia $E_{max}^{f}$ ületada neid tekitanud elektronide energiat $E_{max}^{e}$ (NB: $e$ , $f$ pole siin astmenäitajad, vaid ülaindeksid):

E_{max}^{f} = E_{max}^{e}

Footoni maksimaalne energia avaldub kui

E_{max}^{f} = h f = h \cdot \frac{c}{λ_{r}}

Elektroni maksimaalne energia avaldub kui

E_{max}^{e} = \frac{m v^{2}}{2} = \frac{p^{2}}{2 m}

Nii et

p = \sqrt{2 m E_{max}}

Maksimaalse energiaga elektroni energia avaldub seega kujul

λ_{e} = \frac{h}{p} = \frac{h}{\sqrt{2 m E_{max}}} = \frac{h}{\sqrt{2 m \frac{h c}{λ_{r}}}} = \sqrt{\frac{h λ_{r}}{2 m c}}

Arvutades saame

λ_{e} = \sqrt{\frac{6, 6 \cdot 10^{- 34} J \cdot s \cdot 5 \cdot 10^{- 11}}{2 \cdot 9, 1 \cdot 10^{- 31} k g \cdot 3 \cdot 10^{8} m / s}} = 6 \cdot 10^{- 12} m = 0, 006 n m - -------- - - -------- -

Vastus. Et tekitada röntgenkiirgust minimaalse lainepikkusega $0, 05 n m$ , peab elektronide lainepikkus olema $0, 006 n m$ e. $λ_{e} \approx 0, 1 λ_{r}$ .

Üldiselt võime kasutada lihtsat ligikaudset seost: kui elektron on kiirendatud pingega $U$ volti, on tema lainepikkus

λ = \frac{1, 2 \cdot 10^{- 9}}{\sqrt{U}} m

ehk

λ = \frac{1, 2}{\sqrt{U}} n m

Kuidas kontrollida valemi (4.1 ) kehtivust ja tehtud arvutuste õigsust katsetega? Selleks tuleb mõõta erinevate kiirustega ja massidega mikroosakeste lainete pikkust. Optikast saime teada, et valguse lainepikkust mõõdetakse difraktsioonivõre abil. Võre kallutab teda läbinud kiirt algsuunast kõrvale nurga $α$ võrra, kusjuures $sin α \sim λ / d$ , $d$ on võrekonstant. Seejuures kehtib väiksuse nõue: kaldunud kiiri saab eristada ainult siis, kui võrekonstant ei ületa liialt lainepikkust. Õnneks pakub loodus ise sobivaid võresid ülilühikeste leiulainete mõõtmiseks: need on aatomite korrapärased mikrovõrestikud – kristallid. Kõik erineva kiiruse ja erineva massiga osakeste difraktsiooni uuringud kristallivõrede abil on kinnitanud seose $λ = h / m v$ kehtivust. (Täpsustame: kui $v$ läheneb valguse kiirusele – muidugi selleni eales jõudmata – tuleb kasutada keerukamaid valemeid.)

Valemi (4.1 ) saime esialgu footoni jaoks, samastades $λ$ footonile vastava valguslaine pikkusega. Kuna selgus, et see valem määrab mistahes osakeste leiulaine pikkuse, võime järeldada, et footoni leiulaineks ongi valguslaine, elektromagnetlaine.

1.4.5 Liivaterad ja elektronid

Kas lainelisus on ainult aine algosakeste eriomadus? Ehk saame interferentspildi ka siis, kui suuname liivapritsi joa peenele kaksikpilule? Võibolla pole lihtsalt küllalt tähelepanelik oldud?

Liivatera mass on suurusjärgus $1 m g = 10^{- 6} k g$ . Võtame liivajoa kiiruseks $10 m / s$ . siis saame de Broglie’ valemi järgi lainepikkuseks $λ_{liivatera} = 6, 6 \cdot 10^{- 29} m$ . See on umbes miljard ruudus korda lühem aatomi läbimõõdust. Pole lootustki kunagi teha või leida nii väikesi difraktsioonitõkkeid. Liivaterade, isegi tolmukübemete interferents ja difraktsioon jääb nägemata. Kummatigi pole põhjust arvata, et lainelisus ei oleks kõigi kehade universaalne omadus. Väikestegi makrokehade puhul jääb see varjatuks, ilmub ainult looduse pisimate ehituskivide – algosakeste, veel ka aatomite ja molekulide puhul.

Joon. 4.4. Elektroni jälg magnetvälja asetatud mullikambris (spiraalne, sest kambrit täiva veeldatud vesiniku molekulidega põrkudes kaotab elektron pidevalt energiat).

Fotol joon. 4.4 on elektroni liikumistee jälg mullikambris. Näib, et elektron on käitunud nagu makrokeha, tal on selgesti nähtav trajektoor, laineomadustest pole mingit märki. Jah, aga udujälje jämedus on parimal juhul $0, 1 m m = 10^{- 4} m$ . See on isegi aatomi läbimõõdust miljard korda suurem, mis siis veel elektronist rääkida. Sellise täpsusega ongi määratud elektroni trajektoor. Isegi määratlus “lennuk asub kusagil Aafrika kohal” on palju täpsem. Elektroni trajektoor mullikambris on küllalt täpselt määratud makromaailma mõõtkavas, mitte mikromaailma omas. Kui elektron on suletud aatomi mõõtmetega ruumi, siis juba laineomaduste arvestamiseta läbi ei saa.

Küsimused ja ülesanded

Mis juhtub elektronide interferentsitriipude vahemikega, kui elektronkimbu kiirenduspinget tõstetakse?

answer

Elektronil ja footonil on võrdsed lainepikkused. Millised on nende impulsid?

answer

Millise pingega on elektrone kiirendatud, kui difraktsioonikatsest määrati nende de Broglie’ lainepikkuseks

5, 48 \cdot 10^{- 11} m

answer

Osakesi laenguga

+ e

kiirendatakse difraktsioonikatses pingega

50 k V

. Katsest leiti nende de Broglie’ lainepikkuseks

1, 28 \cdot 10^{- 13} m

. Mis liiki osakesed need on? (Vihje: arvuta osakeste mass ja leia tabelist, millistele osakestele see sobib.)

answer

Arvuta elektroni de Broglie’ lainepikkus, kui tema kiirus on

90 %

valguse kiirusest. (Arvesta, et relatiivsusteooria kohaselt kasvab liikuva elektroni mass valemi

m = \frac{m_{0}}{\sqrt{1 - (\frac{v}{c})^{2}}}

järgi, kus

m_{0}

on seisumass,

v

elektroni kiirus ja

c

valguse kiirus vaakumis. Veendu, et massi muutus avaldub märgatavalt alles valguse kiirusele lähenevatel kiirustel.)

answer

Footoni energia on võrdne elektroni kineetilise energiaga

E_{e} = 100 e V

. Leia mitu korda on footoni lainepikkus pikem kui elektroni lainepikkus.

answer

Milline peaks olema elektroni ja footoni energia, et nende lainepikkused saaksid võrdseks?

answer

Vaskplaadile langeb ultravalgus lainepikkusega

λ_{f} = 200 nm

. Vase väljumistöö

A = 7, 0 \cdot 10^{- 19} J

. Milline on plaadist väljuvate elektronide lainepikkus

λ_{e}

answer

Elektronil ja footonil on võrdsed lainepikkused, kummalgi

0, 2 n m

. Millised on kummagi energiad?

answer

Korraldame võidujooksu prootoni, elektroni ja footoni vahel. Kõikidel on ühesugune lainepikkus. Kuidas järjestuvad nende kiirused (kõige kiiremast kõige aeglasemani)?

answer

Stopp! Jäta meelde!

Mikroosakeste laineomadused

Nii pisitõkkeist mööduvate mikroosakeste kimpude kui ka üksikosakeste tabamusjäljed detektori pinnal korrastuvad interferentsi- või difraktsioonipiltideks. Seega ilmnevad mikroosakeste liikumises laineomadused.

Osakestega seonduvate lainete pikkus

Osakestega seonduvate lainete pikkus on määratav de Broglie' valemist,

λ = \frac{h}{p} = \frac{h}{m v}

mis seob osakeste laineomadusi ( $λ$ ) ja korpuskulaaromadusi ( $m$ , $v$ , $p$ ).

Kehade laineomadused

Laineomadused on kõigi kehade liikumisel, kuid ainult mikroosakeste puhul on lained küllalt pikad, et katses ilmneda.

Leiutõenäosuse lained

Osakeste liikumisel ilmnevad lained on leiutõenäosuse lained, lühidalt leiulained: laine intensiivsus (amplituudi ruut) antud punktis ja hetkel määrab osakese leidmise tõenäosuse selles, kohas ja sellel ajal. Nad ei ole lained mingis keskkonnas.

Osakeste laine- ja korpuskulaaromadused

Osakeste laine- ja korpuskulaaromadused täiendavad üksteist: esimesed avalduvad osakeste liikumisel, teised – nende vastastikmõjudes, nt põrgetes.

Testi ennast!

Elektron lainetab: kas sain aru ja oskan kasutada?

Testi tegemiseks on aega 30 minutit. Tulemused ilmuvad kohe ePortfooliosse.

Open

1.5 Kvantmehaanika ehk lainemehaanika

Saame teada, et

Kui elektron on ka laine, siis kuidas ja kui täpselt on võimalik öelda, kus see laine (elektron) tegelikult asub? Millised on mikromaailma täpsuspiirangud?
Mikromaailmas saab mõnikord teisele poole mäge ilma sellest üle ronimata.

1.5.1 Lainevõrrand mikroosakestele – Schrödingeri võrrand

Räägitakse, et Austria füüsikule Erwin Schrödingerile andis tõuke tema nime kandva võrrandi koostamiseks ühel 1927.a. teaduskonverentsil kellegi noore füüsiku tüütuseni korratud küsimus: “Aga mis ikka toimub lainega, kui osakesele/lainele mõjub jõud?” Schrödingeri võrrand on mikromaailma mehaanika, laine- ehk kvantmehaanika põhivõrrand, nõnda kui makrokehade mehaanika aluseks on Newtoni II seadust matemaatiliselt väljendav võrrand, lihtsustatud kujul:

F = m a

Kui teame mingil hetkel makrokeha asukohta (koordinaate), kiirust ja talle mõjuvaid jõudusid, saame Newtoni II seaduse alusel tema liikumist täpselt kirjeldada, s.o. ennustada tema asendeid järgnevail (või ka määrata eelnevail) hetkil, anda tema kulgemistee ehk trajektoori valemi. Võime kindlalt öelda, kust ta tuleb ja kuhu läheb.

Ilmselt on “laineliste” mikroosakeste liikumise kirjeldamiseks vaja hoopis uut teooriat, mis kirjeldaks leiulainet ja selle ajalist muutumist. Selle teooria lõigi Schrödinger (samaaegselt ja teisel matemaatilisel kujul ka Werner Heisenberg).

Schrödinger lähtus oma võrrandi koostamisel üldisest lainevõrrandist, mis kirjeldab igasuguseid (hääle-, veepinna-, elektromagnet- jne.) laineid ja sulandas selle de Broglie’ seosega

λ = \frac{h}{m v}

Saadud võrrand on diferentsiaalvõrrand, s.o. võrrand, mis sisaldab muuhulgas tuletisi. Diferentsiaalvõrrandi lahendid pole arvud, nagu algebralisel võrrandil, vaid funktsioonid, antud juhul siis leiulainet esitavad lainefunktsioonid. Paraku puudub meil diferentsiaalvõrrandite käsitlemiseks veel matemaatiline ettevalmistus.

Mis on Schrödingeri võrrand

Illustratsiooniks kirjutame välja Schrödingeri võrrandi ühe lihtsaima erijuhu, nimelt võrrandi osakese seisulainele, kui osake liigub üksnes piki x-telge:

\frac{d^{2} Ψ}{d x^{2}} + (\frac{8 π^{2} m}{h^{2}}) (E - V) Ψ = 0

Siin on $Ψ$ osakese leiulaine amplituud, $d^{2} Ψ / d x^{2}$ tähistab selle teist tuletist, s.o. tuletisest võetud tuletist, $E$ on osakese koguenergia, $V = f (x)$ – potentsiaalne energia. Tõdeme, et võrrandi kuju konkreetseteks juhtudeks määrab potentsiaalse energia sõltuvus ruumikoordinaatidest, meie juhul vaid $x$ -st – $f (x)$ .

Schrödingeri võrrandi kaudu, toetudes kaasaegse arvutitehnika abile, saab arvutada leiulaineid osakeste väga erinevateks liikumise ja vastastikmõju juhtudeks.

Muide, ka makrokehade mehaanika rajaneb diferentsiaalvõrrandeil. Newtoni II seadust väljendav algebraline võrrand $F = m a$ on üksnes üldkehtiva diferentsiaalvõrrandi

F = \frac{d p}{d t}

ehk

F = \frac{d (m v)}{d t}

erijuht, mis kehtib, kui jõud, mass ja kiirendus on konstantsed. Alati nad ei pruugi seda olla, näiteks kahaneb lendava raketi mass väljapaiskuvate heitgaaside arvel.

1.5.2 Mikromaailma täpsuspiirangud

Mikroosakeste füüsikas on esialgu veidrana näivaid piiranguid. Nimelt on osakest iseloomustavate suuruste paare, nt osakese asukoht ja impulss, millest kumbagi ei saa ühtaegu määrata suvalise täpsusega. Suurendades ühe määramise täpsust, kaotame alati teise täpsuses. Täpsuspiirang ei ole seotud mõõtevahendite ebatäiuslikkusega. Ta ei ole kõrvaldatav riistade ega meetodite mingi täiustusega. Ta johtub otseselt osakeste laineloomusest. Sarnaseid piiranguid kohtame ka makromaailmas lainenähtusi uurides.

Kujutleme, et meil on magnetofonilint muusikapala salvestusega. Lõikame sellest välja lühikese jupi. Kas saab kuitahes lühikese jupi järgi määrata, mis noote (helisagedusi) mängiti hetkel, kui lindilõik salvestati? Vastus on: ei saa. Liig lühikesse ajavahemikku $Δ t$ mahub liiga vähe võnkeid. Võime jupi kleepida pika tühja lindi vahele (joon. 5.1) ja seda kuulata. Liig lühikesest jupist kuuleme vaid mingit kõlksatust, millest heli ei erista. Kui kasutame täiuslikku helianalüsaatorit, võime küll tuvastada võnkefragmendi graafiku, kuid me ei tea, kas see on lõik siinuslainest (joon. 5.2,a) või hoopis “saehambast”, mis on moodustunud paljude võnkumiste liitumisel (5.2,b). Lainefüüsikas tõestatakse, et igasuguste lainetusimpulsside jaoks kehtib

(5.1)

Δ f = \frac{1}{Δ t}

kus $Δ t$ on impulsi kestus ja $Δ f$ sagedusvahemik, millesse langevad impulsiks liitunud lainete sagedused. (Seose (5.1 ) mõistmiseks uuri tähelepanelikult joonist 5.3)

Joon. 5.3. A. Lihtsaimat lainet, siinuslainet võime iseloomustada kahel erineval viisil: kas ruumiliselt, justkui laine fotona mingil fikseeritud hetkel (punane graafik) või ajaliselt, võnkeprotsessina fikseeritud ruumipunktis (must graafik). B, C: Vaadeldes hulga erineva sagedusega ( $f_{1}, f_{2}, . . .$ ) ja vastavalt erineva lainepikkusega ( $λ_{1}, λ_{2}, . . .$ ) lainete liitumist esimesel viisil, täheldame nende ühinemist piiratud ulatusega ( $Δ x$ ) lainejadaks ehk lainepaketiks (B); vaadeldes nende liitumist teisel viisil, ajaliselt, leiame, et nad võivad liituda piiratud kestusega ( $Δ t$ ) laineimpulsiks (C) Hoiatus: mitte segada sõna impulss kaht eri tähendust: siin tähendab ta lühiajalist ilmingut, värahtust, seevastu mehaanikas tähendas impulss liikumishulka $m v$ .

Sama kehtib ka “laineliste” mikroosakeste kohta. Näiteks footoni energiat

E = h f

ei saa (5.1 ) arvestades määrata täpsemalt kui

Δ E = h Δ f = \frac{h}{Δ t}

ehk

Δ E Δ t = h

kus $Δ t$ on footoni kiirgumise aeg aatomist, kvantsiirde kestus. Väiksema täpsusega muidugi saab, seepärast on õigem kirjutada

(5.2)

Δ E Δ t \geq h

See ongi täpsuspiirang energia- ja ajavahemike jaoks. Võib öelda ka nii: kui põsib mingil energiatasemel vaid ajavahemiku $Δ t$ , ei ole selle taseme energia $E$ määratav täpsemalt kui "paikneb kusagil energialõigu $Δ E = h / Δ t$ piires".

(5.3)

Δ p_{x} Δ x \geq h

Samalaadset piirangut kohtame, kui tahame mingil hetkel ühtaegu määrata osakese $x$ -suunalist kiirust $v_{x}$ (või impulssi $p_{x} = m v_{x}$ ) ja asendit ruumis, koordinaati $x$ . Jällegi osutub, et

Tõepoolest, $p$ on rangelt ja täpselt määratud osakesel, mille leiulaine on alguse ja lõputa siinuslaine. Siis $p_{x} = h / λ$ , $Δ p_{x} \to 0$ , aga me ei tea midagi osakese asukohast ses otsatus laines, $Δ x \to \infty$ . Võime küll paljudest leiulainetest “kokku segada” lainekobara e. lainepaketi (joon. 5.3). Sel juhul on osake hetkeks ruumis lokaliseeritud paketi piiresse ( $Δ x$ ), aga impulss on siis automaatselt paljude igale lainele vastavate impulsside segu (vahemikust $Δ p_{x}$ ).

Täpsuspiirangud formuleeris üks kvantfüüsika loojaid, Saksa füüsik Werner Heisenberg. Tema järgi nimetatakse neid Heisenbergi ebatäpsus-suheteks e. ebatäpsusrelatsioonideks e. lihtsalt Heisenbergi relatsioonideks.

Täpsuspiirangud footonitele

Vaatame mõne näite põhjal, kuidas avalduvad mikromaailma täpsuspiirangud footonitel.

1. Footoni jaoks saame seose (5.3 ) kergesti otse seosest (5.1 ):

Et footoni impulss

p = \frac{h f}{c}

siis

Δ p = \frac{h Δ f}{c}

Δ p = \frac{h}{c Δ t}

Kuna footoni lokaliseerumisala $Δ x$ võime hinnanguliselt võrdsustada $c Δ t$ -ga, saamegi

Δ p Δ x = h

See näitab mõlema täpsuspiirangu ühist päritolu, tulenevust osakese laineomadustest.

2. Vaatame täienduseks veel üht lihtsaimat juhust, kui lainekobara moodustavad kaks lähedase lainepikkusega lainet (joon. 5.4). Siis

Δ x = 5 λ_{1} = 4 λ_{2}

kuna

\frac{Δ x}{l_{1}} - \frac{Δ x}{λ_{2}} = 1

siis

Δ x (p_{1} - p_{2}) = h

(sest $p_{x} = h / λ$ ). Võrdsustades

p_{1} - p_{2} = Δ p

jõuame täpsuspiirangule (5.3 ). Sellele primitiivsele arutelule on muidugi mõndagi ette heita, kuid sama tulemus saadakse ka kvantfüüsika korrektseist arvutusist.

3. Vaatame elektroni difraktsiooni pilul (joon. 5.5). Difrageeruva elektroni y-koordinaat on määratud pilu laiuse $Δ y$ täpsusega, $Δ p_{y}$ on hinnatav esimese difraktsioonimiinimumi järgi:

Δ p_{y} = p sin θ

(vt. joonis). Optikast teame, et

sin θ = \frac{λ}{Δ y}

ehk

Δ y = \frac{λ}{sin θ}

Seega

Δ p_{y} Δ y = p_{y} sin θ (\frac{λ}{sin θ}) = p_{y} (\frac{h}{p_{y}}) = h

1.5.3 Mõõtmised makro- ja mikroilmas

Ristkülikute kõrgus kujutab püstteljel, laius – rõhtteljel märgitud suuruse ebatäpsust (täpsuspiirangut).

Makronähtuste vallas oleme harjunud sellega, et mõõteriistad ei avalda märgatavat mõju mõõdetavale suurusele, või kui avaldavadki, saab seda mõju täpselt arvestada. Ampermeeter ei muuda kuigivõrd voolutugevust vooluringis, täppismõõtmistell arvestatakse tema sisetakistust. Kaenla alla pistetud termomeeter ei jahuta meid märgatavalt jne.

Teisiti on lood mikromaailmas. Kui tahame elektroni asukohta täpsustada temalt hajunud valgust registreerides, peab temalt põrkuma vähemalt üks footon. Aga siis muutub kohe elektroni impulss footonilt põrkel saadu võrra. Mida täpsemalt tahame elektroni lokaliseerida, seda lühemalainelist valgust on vaja, ja seda enam elektroni häiritakse. Võttes hinnanguliselt $Δ x = λ$ ja $Δ p = h f / c$ , kus $λ$ on valguse lainepikkus ja $h f / c$ footoni impulss, leiame taas

Δ x Δ p = \frac{λ h f}{c} = h

sest

λ = \frac{c}{f}

1.5.4 Potensiaalibarjäär ja potensiaaliauk

Joon. 5.6. Potentsiaalibarjäär ja potentsiaaliauk.

Et mikromaailma käsitluses edasi jõuda, põikame jälle korraks makroilma. Kohaku kiirusega $v_{0}$ veerev kuulike oma teel barjääri, "pinnavolti" (joon. 5.6, A). Mäkke tõustes hakkab ta kiirus kahanema, tema kineetiline energia $m v^{2} / 2$ muundub pidevalt potentsiaalseks energiaks $m g H$ . Kui tema algne kineetiline energia

\frac{m v_{0}^{2}}{2} > m g H^{'}

( $H^{'}$ on barjääri kõrgus), veereb ta sellest üle. Vastasel korral,

\frac{m v_{0}^{2}}{2} < m g H^{'}

veereb ta tagasi, otsekui “peegeldub” barjääril. Energia vaatekohast nimetatakse pinnavolti potentsiaaalibarjääriks.

Hakkame nüüd barjääri mõttes järjest kõrgemaks kasvatama (joon. 5.6, B), kuni see piirjuhul kasvab üle iga määra. Siis peaks ka seda ületada üritava kuulikese energia $m v_{0}^{2} / 2$ olema lõpmata suur. Meil oleks siis lõpmata kõrge potentsiaalibarjäär, potentsiaalisein.

Kui kuulike on sulustatud kahe barjääri vahele (joon. 5.6, C), või tõkestatud igast küljest (5.6, D), on ta potentsiaaliaugus. Kui

\frac{m v_{0}^{2}}{2} < m g H^{'}

ei pääse ta august välja, jääb barjääride vahele võnkuma, kuni lõpuks hõõrdumise tõttu peatub augu põhjas.

1.5.5 Tunneliefekt – tunnel ilma tunnelita

Naaseme mikroilma. Leidsime, et pisiosakese jaoks ei mängi gravitatsioonienergia mingit rolli. Potentsiaalibarjääre võivad siin moodustada elektriväljad, kui nende tugevus jaotub ruumis nii, et nad tõkestavad osakese liikumist. Näiteks tekitab positiivse tuuma tõmbejõud potentsiaalibarjääri tuumast eemale pürgivale elektronile.

Lõpmata kõrgest potentsiaalibarjäärist ei saa elektron milgi moel üle. Tähendab, tema leiulaine amplituud peab barjääril muutuma nulliks, laine peab täielikult kustuma, nagu keel seiskub kinnituskohas. Barjääri poole liikuv osake paiskub barjäärilt tagasi.

Teisiti on lugu lõpliku kõrgusega barjääril. Vastav Schrödingeri võrrand näitab, et siis ulatub leiulaine pisut ka barjääri sisse, kuigi selles kiiresti kahanedes (joon. 5.7). Kui barjäär on väga õhuke (hinnaguliselt – umbes osakese lainepikkuse suurusjärgus), võib leiulaine levida läbi barjääri, jatkudes teisel pool taas siinuslainena, kuigi tublisti kahanenud amplituudiga (leiutõenäosusega). See tähendab, et on lõplik tõenäosus leida osakest teispool barjääri ka siis, kui tema energia ei küüni potentsiaalibarjääri kõrguseni. Piltlikult: elektron justkui uuristaks tunneli läbi barjääri. Tegelikult pole muidugi mingit tunnelit, on vaid mikroosakese lainelisusest tingitud kummaline efekt. Võrdlusest on ta nimegi saanud – tunneliefekt.

Joon. 5.7. Elektroni leiulaine levib läbi õhukese barjääri.

Üks aatomituumade radioaktiivse lagunemise viise – alfalagunemine – on tunneliefekt. Alfaosakesed väljuvad tuumast “tunneleerudes”. Väga tugevas (umb. $\leq 10^{9} V / m$ ) elektriväljas väljuvad elektronid ka kuumutamata ja valgustamata katoodist. See on külmemissioon, üks tunneliefekti avaldusi. Järgmises punktis kohtame üht külmemissiooni paeluvaimat rakendust – tunnelmikroskoopi. Tunneliefekti rakendatakse mitmeti nüüdiselektroonikas.

Küsimused ja ülesanded

Proovi leida suuruste paare väljaspoolt füüsikat, millele kehtivad täpsuspiirangudte taolised seosed (nt. sõna tähenduse määratlustäpsus - sõna kasutatavus teabekandjana - vrdl. nt. sõnu naine-pruut-Kaie- eks kasva ses reas määratlustäpsus ja kahene kasutusvaldkond).

answer

Kas elektronide tiirlemine kindlatel orbiitidel oleks kooskõlas kvantfüüsika täpsustpiirangutega?

answer

Stopp! Jäta meelde!

Kvantmehaanika ehk lainemehaanika

Laineomadustega mikroosakeste ja nende kogumite käitumist käsitlev füüsika osa on kvantmehaanika e. lainemehaanika.

Schrödingeri võrrand

Kvantmehaanika teoreetiliseks aluseks on Schrödingeri võrrand –diferentsiaalvõrrand, mille kaudu saab arvutada osakese leiulaine sõltuvuse koordinaatidest ja ajast, kui on teada osakese mass ja talle mõjuvad jõud.

Mikroosakeste siseomased täpsuspiirangud

Mikroosakeste laineomadustest tulenevad neile siseomased täpsuspiirangud (Heisenbergi ebatäpsussuhted): on osakest iseloomustavate suuruste paare, milles kumbagi suurust ei saa korraga mõõta suvalise täpsusega; ühe minimaalne mõõteviga on pöördvõrdeline teise suuruse mõõteveaga. Sellisteks paarideks on nt impulss ja koordinaat, energia ja aeg:

Δ p_{x} Δ x \geq h

Δ E Δ t \geq h

Testi ennast!

Kvantmehaanika ehk lainemehaanika: kas sain aru ja oskan kasutada?

Testi tegemiseks on aega 60 minutit.

Open

1.6 Kvantmehaanika töötab

Siin saame teada

Kuidas töötab mikroskoop, milles kujutise moodustavad footonite (valguse) asemel elektronid.
Kuidas on veel võimalik "näha" asju, mida ei ole võimalik näha.
(Mis on ja kuidas töötab välkmälu.)

1.6.1 Elektronmikroskoop

Elektronmikroskoobis ei kasutata objekti läbivalgustamiseks valgusvihku, vaid seda kiiritatakse läbi elektronkimbuga. Objektist tekitavad suurendatud kujutise elektronläätsed. Need on torujad elektromagnetid (joon.6.1), mille õõnt läbides elektronkimbud koonduvad niisama kui valguskiired klaasläätsede toimel. Elektronläätsedega tekitatud kujutis tehakse nähtavaks luminestseerival ekraanil või jäädvustatakse fotoplaadil (filmil). Joonisel 6.2 võrreldakse elektronmikroskoopi tavalise optilise mikroskoobiga.


Joon. 6.1. Magnetelektronlääts lõikes.	Joon. 6.2. Tavalise valgusmikroskoobi ja elektronmikroskoobi võrdlus.

Elektronmikroskoop suurendab uuritavaid objekte sadu kordi tugevamini kui valgusmikroskoop. Mikroskoobi suurendusvõimet piirab difraktsiooninähtus, mis muudab pisidetailid hägusaks. Üldiselt ei saa eristada mikroskoobis kasutatava kiirguse poollainepikkusest väiksemaid detaile. Difraktsioon sõltub lainepikkusest. Väiksemaid detaile saab eristada seda selgemalt (lahutusvõime on seda suurem), mida lühemalainelises kiirguses objekte vaadeldakse. Elektronilained on valguslainetest palju lühemad. See annabki neile mikroskoopias eelise. Elektronide lainepikkus on seda väiksem, mida tugevamas elektriväljas nad on kiirendatud (p. 4). Seepärast rakendatakse elektronmikroskoobis kõrgpinget, enamasti 100 000 V suurusjärgus. Kuid on ka hiidmikroskoope, kus pinge ulatub miljoni voldini. Paksematest objektidest, mida elektronid ei läbista, valmistatakse õhukesed jäljendid: nende pinnale aurustatakse süsinikust või kullast kelme, mis pinnast eraldatakse. See meenutab kipsjäljendite võtmist bareljeefidelt. Elektronmikroskoobiga saab hästi vaadelda baktereid, viiruseid, kristallipinna atomaarseid defekte jpm.

TÜ Füüsika Instituudis paiknev kõrglahutusega analüütiline läbivalgustav elektronmikroskoop (HR-TEM). Sellise seadmega saab määrata tahkete/kondenseerunud materjalide struktuuri ja osakeste/kristalliitide suurust, uurida defekte jpm. Seadme ruumiline lahutus on kuni $0, 08 n m$ kristalliliste ainete puhul. Uurimiseks tuleb objektidest valmistada sub-mikromeetrilise paksusega õhikud või sadestada nanoosakesed spetsiaalsetele alustele, seejärel viia objekt koos spetsiaalse hoidjaga objektikambrisse, kõrgvaakumi keskkonda.

Joon. 6.3. Raster-elektronmikroskoobi tööpõhimõte.

Rastermikroskoobis (joon.6.3) teravustatakse elektronkiir elektronläätsedega objekti pinnale mikrotäpiks (umb. 1 μm²). Kallutuspoolid hälvitavad kiirt rida-realt üle terve uuritava pinna (skaneerimine, nagu pildilaotus televiisoris). Objekti lähedal on tajur, mis “aistib” objekti pinnalt tagasi põrkunud või langevate elektronide mõjul objektist välja paisatud elektrone (viimased on teisesed e. sekundaarelektronid; meenutame, et dünoodidest välja paisatud sekundaarelektronid võimendavad fotoelektronide voogu fotoelektronkordistis, vt Optika, lk. 83). Pinna mikroreljeef, samuti keemiline koostis muudavad täpp-täpilt nii põrkunud kui ka sekundaarsete elektronide voogu. Tajur on ühendatud kuvariga, mille ekraanile ilmubki kujutis. Rastermikroskoobi suurendused ei küüni elektronmikroskoobi omadeni. See-eest annab ta suure sügavusteravuse, kujutised näivad lausa ruumilistena. Temaga vaadeldakse ja pildistatakse edukalt nt. väikeorganisme ja nende organeid, tehnikaseadiste mikrodetaile jpmt.

Joon. 6.4. Tunnelmikroskoobi (nanoskoobi) põhimõttevisand (skaneerimissõlm on tegelikult arvutist kümneid kordi väiksem).

Elektronmikroskoopia viimane sõna on rastermikroskoobi eriliik, tunnelmikroskoop. Selles skaneerib objekti pinda üliteravaks (üksikaatomini tipus) söövitatud metallteravik. Seadme põhimõte meenutab mõnevõrra merepõhja reljeefi kaardistamist nöörloodi abil. Teravikule antakse objekti suhtes mõnevoldine negatiivne potentsiaal. Kui teravik viia objektile väga lähedale (0,1 - 1 nm), hakkab ta kiirgama elektrone, tekib külmemissioon e. autoemissioon (lk. 31). Selle põhjuseks on kvantmehaaniline tunneliefekt, mis ongi riistale nime andnud. Teravikku hoiab ja juhib piesoelektrilisest materjalist kolmsõrmik (joon. 6.4), mida omakorda käsutab arvuti. Piesoelektrikud muudavad neile rakendatud elektriväljas pisut oma mõõtmeid, seeläbi nõela liigutades. Sellal kui sõrmiku harud X ja Y skaneerivad pinda, hoiab vertikaalharu Z nõela pinnast konstantsel kaugusel, nõnda et emissioonvool ei muutuks. Seda saab teha ülitäpselt, sest tunnelvool sõltub tugevasti vahekaugusest: 0,1 nm nihe muudab voolu ca 100 korda. Pinna mikroreljeef ilmub kuvari ekraanile. Reljeefi kajastab haru Z nihutamispinge koos skaneerimispingetega. Jälgitavad on aatomi mõõtmeist palju väiksemad nõela püstnihked – kuni 0,001 nanomeetrini. Horisontaalsuunas ulatub parim lahutus 0,1 nanomeetrini, mis kuvariekraanil annab umbes 1 cm, nii et kogusuurendus tuleb 10⁸ X.

Niisiis “nähakse” tunnelmikroskoobi abil üksikaatomeid, saadakse jälgida nende paiknemist aine pinnal (vt. kaanepilti ja joon. 6.5). Tunnelmikroskoop (ja selle mitmed uusimad teisendid) on aatomimikroskoobid. Õigem olekski riista nimetada hoopis nanoskoobiks või koguni pikoskoobiks, sest tema ersitusvõime küünib nanomeetreist kümnete pikomeetriteni. Ta on asendamatu ainete (nt. pooljuhtmaterjalide) pinnastruktuuri ja selle atomaardefektide vaatlemiseks, on elektronmikroskoopia rekordiomanik, tippsaavutis. Vähe sellest, tunnelmikroskoobi abil saab pinda aatomite viisi kujundada, aatomeid pinnal vajalikul viisil ümber paigutada.

Elektronmikroskoop Tartu Teaduspargi Nanolab'is.

Kui tunnelmikroskoobiga saab uurida vaid küllalt hea elektrijuhtivusega objekte, siis tema edasiarendusel, aatomjõumikroskoobil, seda kitsendust pole. Objekti pinda kombatakse selleski teravikuga, kuid seda hoiavad pinnast kindlal kaugusel piesotäiturid, mis reageerivad ülitundlike jõumõõturite signaalile. Viimased mõõdavad nt. liibumisjõude pinna-aatomite ja teraviku tipuaatomi vahel.

Elektronmikroskoobi leiutas 1930ndail aastail Saksa insener Ernst Ruska (1906-1988), rasterelektronmikroskoobi umbes samal ajal sakslane Max Knoll, esimese tunnelmikroskoobi tegid 1981 šveitslased Heinrich Rohrer (s. 1933) ja Gerd Binnig (s. 1947). 1986 kroonis Ruska, Rohreri ja Binnigi saavutusi elektronmikroskoopias Nobeli füüsikapreemia.

Küsimused ja ülesanded

Ka röntgenikiirgus on valgusest, ultravalgusestki palju lühema lainepikkusega. Miks ei kasutata röntgenmikroskoope?

answer

Stopp! Jäta meelde!

Elektronmikroskoopide kujutis

Elektronmikroskoopides tekitatakse objekti suurendatud kujutis elektronkimpude abil.

Läbivkimbu elektronmikroskoobi tööpõhimõte

Läbivkimbu elektronmikroskoobi põhimõtteskeem sarnaneb valgusmikroskoobi omale, ainult valgusvihud on asendatud elektronkimpudega, läätsed – elektronläätsedega. Saadavad suurendused ületavad sadu kordi parimagi optilise mikroskoobi omi, sest elektronide lainepikkus on paju väiksem valguslainete pikkusest.

Rastermikroskoobis

Rastermikroskoobis skaneeritakse objekti pinda tugevasti teravustatud elektronkimbuga. Kujutis saadakse kuvari ekraanil ja ta kajastab langeva elektronkimbu mõjul objekti eri punktidest väljuvate sekundaarelektronide voo intensiivsust

Tunnelmikroskoop

Tunnelmikroskoobis skaneeritakse objekti selle pinna ligidal hoitava ülipeene teravikuga, kujutis tekib kuvari ekraanil teraviku ja objekti vahelise tunnelvoolu (külmemissioonivoolu) kaudu. Tunnelmikroskoop teeb nähtavaks objektide aatomstruktuuri.

Testi ennast!

2 Elektronid aatomis

2.1 "Laineline" elektron aatomis

Siin saame teada

Kuidas elektronide lainelised omadused annavad selgituse aatomi energiatasemete diskreetsusele ja Bohri aatomimudelile.
Millised energiatasemed on aatomites olemas.
Milline on perioodilisustabeli füüsikaline põhjendus.

2.1.1 Elektron karbis

Oleme küllaldaselt tutvunud elektroni kui mikroosakese omadustega, et tagasi pöörduda aatomi siseehituse juurde.

Aatomist ei lase elektrone lahkuda positiivselt laetud tuuma tõmbejõud, mis tekitavad elektronile sügava potentsiaaliaugu. Elektroni leiulained on selles “augus” sulustatud ja peavad muunduma seisulaineteks, nõndasamuti kui elastsuslained otstest kinnitatud pillikeelel. Nende seisvate leiulainete kuju täpne kvantmehaaniline arvutus on keerukas ja väljub selle kursuse raamest.

Et saada ülevaatlikku pilti põhimisest, käsitleme aatomi lihtsustatud mudelit. Sulustame elektroni tõmbejõudude asemel igast küljest seintega, mis elektronile läbimatud. Ta on siis ülisügavas potentsiaaliaugus. Moodustagu seinad kuubi, külje pikkusega $L$ (joon. 7.1). Alustame juhust, kui elektron liigub kuubis ühe tahkudepaari vahel, nendega ristsuunas. Kuna elektron ei pääse seintest läbi, peab tema leiulaine amplituud tahkudel kahanema nulliks, nagu keele võnked kinnituspunktides. Meil on siis heliseva keele täpne analoog. Samuti kui keele võnked (vrd. seoseid (3.2 )), on elektroni leiulained kuubis seisulained pikkusega

(7.1)

λ_{n} = 2 \cdot \frac{L}{n_{L}}, n_{L} = 1, 2, 3 . . .

Asendades $λ$ de Broglie’ seosest

λ = \frac{h}{m v}

saame

\frac{h}{m v_{n}} = 2 \frac{L}{n_{L}}

ehk

(7.2)

v_{n} = (\frac{h}{2 m L}) \cdot n_{L}

kus $v_{n}$ on elektroni kiirus seisulaines pikkusega $λ_{n}$ . Näeme, et erinevalt makrokehast, mis võiks potentsiaaliaugus omandada suvalisi kiirusi, tohib sulustatud mikroosake liikuda ainult teatud kindlate kiirustega $v_{n}$ , tema kiirus on kvanditud.

Eeldame veel, et elektroni potentsiaalne energia kuubi sees on konstantne, $E_{p} = c o n s t$ . Alati võime valida $c o n s t = 0$ , sest füüsikanähtused sõltuvad vaid energia vahedest, mitte absoluutväärtustest. Siis on elektroni koguenergia tervenisti kineetiline, $m v^{2} / 2$ , ja valemi (7.2 ) järgi leiame pikemata seisulainetele $λ_{n}$ vastavate energiatasemete $E_{n}$ redeli:

(7.3)

E_{n} = (\frac{h^{2}}{8 m L^{2}}) n_{L}^{2}, n_{L} = 1, 2, 3 . . .

Saimegi katkendlikult, diskreetselt jaotunud energiatasemed. Joonisel 7.2 on kujutatud mõned madalaimad neist, koos vastavate leiulainete ja nendega määratud leiutõenäosustega.

Joon.7.2. Läbistamatute seinte vahele (sügavasse potentsiaaliauku) sulustatu elektroni madalaimad energiatasemed, leiulained ψ ja leiutõenäosused ψ² . Iga energiatase on võetud ühtlasi vastava ψ ja ψ²

Nüüd taipame, kuidas elektronide laineomaduste tõttu tulevad mängu täisarvud $n_{L}$ , mida kvantfüüsikas nimetatakse kvantarvudeks. Laineomadustega elektron ei saa karbis kunagi paigale jääda, tema madalaim energia ei ole $0$ , vaid

E_{1} = (\frac{h^{2}}{8 m L^{2}})

See on elektroni põhiseisund. Kui $n_{L} = 2, 3, 4...$ , on elektron ergastatud seisundites. Põhiseisundile vastab lihtsaim seisulaine, mille üksainus poollaine mahub parajasti karpi. Suurima tõenäosusega leiame elektroni siis karbi keskelt.

Üldjuhul, kui elektroni kiirusvektor $\to v$ on karbis suvaliselt suunatud, võime seda kujutleda kolme, koordinaattelgedega paralleelse komponendi

{\to v}_{x}, {\to v}_{y}, {\to v}_{z}

vektorsummana (joon. 7.1 B). Leiulaine liitub siis kolmest osalainest. Iga osalaine moodustab seisulaineid pikkusega

\begin{matrix} λ_{x} = \frac{2 L}{n_{x}} = \frac{h}{m v_{x}}, n_{x} = 1, 2, 3 . . . λ_{y} = \frac{2 L}{n_{y}} = \frac{h}{m v_{y}}, n_{y} = 1, 2, 3 . . . λ_{z} = \frac{2 L}{n_{z}} = \frac{h}{m v_{z}}, n_{z} = 1, 2, 3 . . . \end{matrix}

Valemi (7.3 ) asemel kirjeldab nüüd energiatasemeid seos

(7.4)

E^{'} = (\frac{h^{2}}{8 L^{2} m}) (n_{x}^{2} + n_{y}^{2} + n_{z}^{2})

Näeme, et kolmemõõtmelises ruumis määravad energiatasemed kolm kvantarvu $n_{x}$ , $n_{y}$ ja $n_{z}$ , mis kõik võivad üksteisest sõltumatult omandada täisarvulisi väärtusi. Seisulaineid kolmemõõtmelises ruumis on raske lehepinnal näitlikult kujutada, seepärast peame piirduma mõnede lihtsaimate kahemõõtmeliste, s.o. pinnalainete kujutamisega (joon. 7.3).

Joon. 7.3. Seisulainete hetkpildid pinnal, nt. kandilisel trummil või ruutu sulustatud elektroni puhul.

Paneme tähele, et ühele ja samale energiatasemele $E_{n}^{'}$ võib vastata mitu erinevat kvantarvude kombinatsiooni. Näiteks saame täpselt sama $E_{n}^{'}$ väärtuse, kui

n_{x} = 1, n_{y} = 2, n_{z} = 3

või kui

n_{x} = 2, n_{y} = 1, n_{z} = 3

Siis öeldakse, et tase $E_{n}^{'}$ on kuuekordselt kidunud: seisulainete vorm on küll erinev, kuid neile kõikidele vastab sama energia. Kidumine kõrvaldatakse, kui milgi viisil on tekitatud eelistatud või eristatavad ruumisuunad, nt. kui kuubi asemel võtame risttahuka küljepikkustega $L_{1}$ , $L_{2}$ , $L_{3}$ , siis

E_{n}^{''} = (\frac{h^{2}}{8 m}) [(\frac{1}{L_{1}^{2}}) n_{x}^{2} + (\frac{1}{L_{1}^{2}}) n_{y}^{2} + (\frac{1}{L_{1}^{2}}) n_{z}^{2}]

2.1.2 Elektronlained orbiidil. Bohri aatom

Elektroni leiulaineid ei sulusta aatomisse muidugi mitte kujuteldava karbi seinad, vaid elektrilised tõmbejõud tuuma ja elektroni(de) vahel. Astume sammu karbimudelilt tegelikkusele lähemale ja üritame sobitada elektroni laineloomust aatomi planetaarmudeliga. Vaatame lihtsaimat, vesiniku aatomit ainsa elektroniga ringorbiidil raadiusega $r$ (joon. 7.4). Kui elektron tiirleb orbiidil, peavad tema leiulained olema orbitaallained, s.o. tiirutama orbiiti pidi ümber tuuma. Elektroni statsionaarsetele, püsiseisunditele vastavad seisulained.

Joon. 7.4. Elektronlaine ringorbiidil. Juhul A üksteisele järgnevad lained ühtuvad, lainete tõusuinterferents tekitab püsiva seisulaine. Juhul B kustutab mõõnainterferents laine, elektroni leiutõenäosus kahaneb nulliks, püsiolekut ei teki.

Otsteta ringil saavad orbitaallaineist tekkida seisulained ainult siis, kui laine ringeldes end lakkamatult kordab (joon. 7.4). Selleks peab ringile sobituma parajasti täisarv laineid:

(7.5)

2 π r = n λ, n = 1, 2, 3 . . .

Asendades $λ$ de Broglie’ valemist (4.1 ), saame

2 π r = n \cdot \frac{h}{m v}

ehk

(7.6)

m v r = n \cdot \frac{h}{2 π} = n \cdot ℏ

kus tähistasime, nagu kvantfüüsikas tavaks,

ℏ = \frac{h}{2 π}

$m$ on elektroni mass, $v$ – tema kiirus. (Meenutame mehaanikakursusest, et $m v r$ on tiirleva elektroni pöördimpulss e. impulssmoment.) Seega on orbiidi raadius $r$ ja elektroni orbitaalkiirus $v$ , siis ka energia, vastastikuses sõltuvuses. Avaldades $r$ valemist (7.6 ), näeme et püsiseisundeile sobivad üksnes

(7.7)

\begin{matrix} r_{1} = 1 \cdot \frac{ℏ}{m v_{1}} r_{2} = 2 \cdot \frac{ℏ}{m v_{2}} r_{3} = 3 \cdot \frac{ℏ}{m v_{3}} \dots r_{n} = n \cdot \frac{ℏ}{m v_{n}} \end{matrix}

kus kvantarvuks on $n = 1, 2, 3...$ .

Elektroni laineomadused ja orbiidid

Seega järeldub elektroni laineloomusest, et ta võib tuuma ümber tiirelda vaid teatud kindlatel orbiitidel raadiusega $r_{n}$ .

Joon. 7.5. De Broglie laine mehaaniliseks analoogiks võiks olla kahest otsast kinnitatud keele võnkumine, aga veel parem on vaadata võnkuvat rõngast. Rõngal saab püsiv seisulaine tekkida siis, kui sinna sobitub täisarv lainepikkusi. Bohri mudeli orbiite peeti ringikujulisteks ja oli loogiline arvata, et lubatud orbiidid on need, kuhu mahub täisarv elektroni seisulaine lainepikkusi. Kuigi selle laine iseloomu kohta ei olnud veel midagi teada, sobis de Broglie elektronlaine mudelisse väga hästi.

Valemi (7.6 ) avaldas 1913. a. esimesena üks maailma tippfüüsikuid, taanlane Niels Bohr (l. nils boor). Tollal ei teadnud ta midagi elektroni laineomadustest. Toetudes vaid intuitsioonile ning soovides seletada aatomi püsivust ja spektraalseeriaid, ta lihtsalt postuleeris (ld. k. postulare - nõudma), et lubatud orbiitidel, mille raadius rahuldab seost (7.6 ), elektronid ei kiirga, kuigi tiirlevad (Bohri I postulaat). See oli muidugi järsus vastuolus makrofüüsika seadustega ja kohtas füüsikkonnas laialdast umbusku. Kuid nõnda õnnestus Bohril “päästa” planetaarmudel kiirgusvaringust (vt. alajaotus 1.2). Sündis uus, Bohri aatomimudel (joon.7.7 c), mis on mänginud mikrofüüsika arengus väga tähtsat osa. Lainesisu (vastavalt valemeile (7.5 ) ja (7.7 )) andis sellele postulaadile 10 aastat hiljem L. de Broglie.

Kesktõmbe- e. tsentripetaaljõuksjõuks $F$ , mis hoiab elektroni tuuma ümber tiirlemas, on elektrijõud tuuma ja elektroni vahel (joon. 7.6). Coulombi seaduse järgi

F = \frac{κ e^{2}}{r_{n}^{2}}

kus $e$ on elementaarlaeng, $κ = \frac{1}{4 π ε_{0}}$ ja $ε_{0}$ elektriline konstant. Teatavasti kesktõmbekiirendus

a = \frac{v_{n}^{2}}{r_{n}}

Rakendades Newtoni II seadust $F = m a$ , saame

F = \frac{m v_{n}^{2}}{r_{n}}

Seega

(7.8)

\frac{κ e^{2}}{r_{n}^{2}} = \frac{m v_{n}^{2}}{r_{n}}

kust saab arvutada orbiitidele raadiusega $r_{n}$ vastavad energiatasemed $E_{n}$ . Tulemuseks on

(7.9)

E_{n} = - \frac{2, 17 \cdot 10^{- 18}}{n^{2}} J = - \frac{13, 6}{n^{2}} e V

Miinusmärk johtub sellest, et nullnivooks loetakse elektroni potentsiaalne energia, kui ta on tuumast eemaldatud lõpmata kaugele. Joonisel 7.7 on valemi (7.9 ) järgi arvutatud energiatasemete skeem.

Bohri II postulaadi järgi kiirgab või neelab aatom valgust ainult elektroni hüpetel lubatud orbiitide vahel (joon.7.7), kusjuures tekivad või kaovad footonid energiaga

(7.10)

h f = E_{k} - E_{m}

kus $E_{k}$ on mingi kõrgema ja $E_{m}$ madalama taseme energia.

Joon. 7.7. Atomaarse vesiniku spektrijooned (a) ja neid tekitavad siirded (b) vesinikuaatomi energiatasemete vahel. Punktiiris – seeriate serv. (c) Bohri – de Borgile´mudeli mõned "lubatud" orbiidid ja siirded nende vahel.

Vastaku kõrgemale tasemele kvantarvu $n$ väärtus $n_{2}$ , madalamale $n = n_{1}$ . Siis, asendades $E_{k}$ ja $E_{m}$ (7.9 )-st, saame

(7.11)

\begin{matrix} h f & = & 2, 17 \cdot 10^{- 18} (\frac{1}{n_{1}^{2}} - \frac{1}{n_{1}^{2}}) J & = & 13, 6 \cdot (\frac{1}{n_{1}^{2}} - \frac{1}{n_{1}^{2}}) e V \end{matrix}

ehk, kuna $λ f = c$ ,

(7.12)

\frac{1}{λ} = 1, 097 \cdot 10^{7} (\frac{1}{n_{1}^{2}} - \frac{1}{n_{1}^{2}}) m^{- 1}

Võrreldes äsja leitud valemit (7.12 ) p. 3 toodud Balmeri-Rydbergi valemiga (3.1 ), mis saadud katses mõõdetud spektrite töötlemisel, näeme oivalist kokkulangevust. Järelikult kirjeldab Bohri - de Broglie’ aatomimudel vesiniku aatomit päris hästi. Ta selgitab mitte üksnes vesiniku joonspektrite tekkepõhjust ja struktuuri, vaid näitab õigesti kätte ka joonte lainepikkused.

Valemi 7.9 tuletamine

Huvilistele, kes väikest rehkendust paljuks ei pane, toome ära ka valemi (7.9 ) tuletuskäigu. Lähtume avaldistest (7.7 ) ja (7.8 ). Avaldame neist $r_{n}$ . Mugavamaks teisendamiseks viime (7.8 ) kujusse

\frac{m^{2} v_{n}^{2}}{m} = \frac{κ e^{2}}{r_{n}}

Siit, avaldades $m_{2} v_{n}^{2}$ (7.7 )-st,

\frac{n^{2} ℏ^{2}}{r_{m}^{2}} = \frac{κ e^{2}}{r_{n}}

millest

(7.13)

r_{n} = \frac{ℏ^{2}}{κ m e^{2}} \cdot n^{2}

Elektroni koguenergia $E_{n}$ $n$ -dal statsionaarsel orbiidil $r_{n}$ liitub tema kineetilisest energiast $E_{k i n} = m v_{n}^{2} / 2$ ja potentsiaalsest energiast tuuma elektriväljas, mis avaldub kuju $E_{p o t} = - k e^{2} / r_{n}$ :

E_{n} = \frac{m v_{n}^{2}}{2} - \frac{κ e^{2}}{r_{n}}

Võrrandist (7.8 ) leiame

\frac{m v_{n}^{2}}{2} = \frac{κ e^{2}}{2 r_{n}}

seega

E_{n} = - \frac{κ e^{2}}{2 r_{n}}

Teisendades avaldist (7.7 ), saame

v_{n} = \frac{n ℏ}{m r_{n}}

Asetades $v_{n}$ sel kujul valemisse (7.8 ), osutub, et

(7.13)

r_{n} = \frac{ℏ^{2}}{κ m e^{2}} \cdot n^{2}

Asendades $r_{n}$ (7.13 )-st leitu koguenergia valemisse, tuleb välja

E_{n} = - \frac{κ^{2} m e^{4}}{2 ℏ^{2}} \cdot \frac{1}{n^{2}}

ehk

(7.14)

E_{n} = - \frac{m e^{4}}{8 ε_{0}^{2} h^{2}} \cdot \frac{1}{n^{2}}

Asendades konstandid $m$ , $e$ , $ε_{0}$ ja $h$ nende arvväärtustega, saamegi valemi (7.9 ).

2.1.3 Kvantfüüsika aatomipilt

Mõned Schrödingeri võrrandi lahendeina saadud elektroni seisulained vesiniku aatomis on kujutatud joon.7.8. Neid pilte võib käsitada kui mitme-miljardikordse suurendusega pildistusi aatomist. (Justkui aegfotod pimedas ümber tänavalaterna tiirutavast ööliblikast – elektron liblika osas.) Muidugi pole aatomit võimalik niiviisi pildistada. Pildid on arvutustulemuste graafiline esitus. Nende tõepära kinnitab neist tulenevate järelduste kooskõla katseandmetega, eriti spektritega. Kujutise heledus sümboliseerib elektroni tabamistõenäosust $[Ψ (x, y, z)]^{2}$ vastavas ruumipunktis. Kujutised meenutavad udu- või suitsupilvekesi. Sageli nimetataksegi neid elektronpilvedeks. Mis on jäänud elektroni “lubatud” orbiitidest? Ainult see, et kui arvutada elektroni tõenäoseim kaugus tuumast igas pilves, siis ühtib see hästi lubatud orbiitide raadiustega. Jäänukina kasutatakse ka nende pilvede kohta vahel nimetust orbitaal.

Nii näeksid välja vesiniku aatomi elektronpilved, kui neid saaks vaadelda – elektroni seisvad leiulained põhiseisundis $1 s$ ( $n = 1$ , $ℓ = 0$ ) ja mõningais madalamais ergastusseisundeis.

Nagu kolmemõõtmeses kuubis, nii ka kolmemõõtmeses aatomis määratlevad elektroni iga võimalikku seisulainet kolm kvantarvu: peakvantarv $n = 1, 2, 3...$ , kõrval- e. orbitaalkvantarv $ℓ = 0, 1, 2... (n - 1)$ ja magnetkvantarv $m_{ℓ} = 0, \pm 1, \pm 2... \pm ℓ$ .

Et aga aatomis ei sulusta elektronilaineid mitte kuubiku tahud, vaid kerasümmeetriaga elektrijõud, tähendavad need kvantarvud hoopis muud kui arvud $n_{x}$ , $n_{y}$ ja $n_{z}$ kuubikus. seepärast on kummagi kvantarvude komplekti tähisedki valitud erinevad. Seisulained, mis nüüd tekivad, on sootuks erinevad kuubis kujunevaist. Eks erine ka lainemustrid veepinnal neljakandilises paagis ja ümaras panges.

Kvantarv $n$ eristab seisulaineid, mis on moodustunud keralaineist (radiaalselt levivaist laineist). Need sarnanevad vette kukkunud kivikesest levivate ringlainetega, kui püüda noid kujutleda kolmes mõõtmes levivaina.

Orbitaalkvantarv $ℓ$ määratleb orbitaallaineid, mis on sündinud tuuma läbiva telje ümber ringlevaist laineist (neid käsitlesimegi eelmises punktis). Kuna $ℓ$ on seotud elektroni tiirlemisega, määrab ta ühtlasi elektroni orbitaal-impulssmomendi (pöördimpulsi) $L$ .

Lõpuks, magnetkvantarv ml määrab orbitaallainete tiirlemistelje (pöördimpulssmomendi vektori $L$ ) orientatsiooni ruumis. Elektroni seisulaine tervikuna moodustub radiaalselt ja orbitaalselt kulgevate lainete summana.

Elektronilainete kuju ning asetus tuuma suhtes sõltub kõigist kolmest kvantarvust. Elektroni keskmise kauguse tuumast ja seega energiataseme määrab aga eeskätt peakvantarv $n$ , $ℓ$ -st sõltub see vähem, ml-st tavaolekus üldse mitte. Vesinikuaatomis on tasemed $ℓ$ suhtes tugevasti kidunud, sama $n$ juures nihutab muutus neid vaid umb. tuhandikosa taseme energiast. Seda pisinihet võib märgata spektrijoonte peenstruktuuris, mille toob ilmsiks tugeva lahutusvõimega spektraalriist. Seepärast õnnestuski vesiniku spektrijooni hästi liigitada üksnes ühe kvantarvu varal, mis rangelt võttes polnud muidugi päris korrektne. Mitme elektroniga aatomites on sõltuvus l-st palju tugevam, ilmneb selgesti ka mõõduka lahutuse juures.

Tasemete kidumise $m_{ℓ}$ suhtes kõrvaldab väline magnetväli (samuti kui kuubiku muutmine risttahukaks - alajaotus 2.1.1). Kui viime kiirgavad aatomid tugeva magneti pooluste vahele ja siis uurime nende spektrit hea lahutusega spektroskoobiga, täheldame spektrijoonte üliväikest lõhenemist (Zeemani efekt, avastaja, hollandlase Pieter Zeemani [1865-1943] järgi).

Lõhede laius on võrdeline magnetvälja induktsiooniga, nende arvu määrab magnetkvantarv $m_{ℓ}$ , sellest nimetuski. Ringlev elektron on võrdväärne pisikese vooluringiga, millega kaasneb alati magnetväli. See astub vastastikmõjusse välisväljaga, just nagu rootori ja püsimagneti magnetväljad elektrimootoris. Vastastikmõju suunabki tiirlemistelge ja nihutab energiatasemeid. Telje võimalikud, hüppeliselt muutuvad kalded välisvälja suhtes kvantiseerib $m_{ℓ}$ .

Schrödingeri võrrandit lahendades selgub, et $n$ võib omandada suvalisi täisarvulisi väärtusi

(7.15)

n = 1, 2, 3, . . .

kuid $ℓ$ ja $m_{ℓ}$ võimalikud väärtused on piiratud:

(7.16)

ℓ = 0, 1, 2... (n - 1)

m_{ℓ} = - ℓ, - (ℓ - 1) . . . - 1, 0, 1, . . . (ℓ - 1), ℓ

ehk

(7.17)

m_{ℓ} = 0, \pm 1, \pm 2... \pm ℓ

Tiirlemine võib toimuda nii päri- kui vastupäeva, sellest $m_{ℓ}$ $\pm$ -väärtused. Kvantarvu $ℓ$ väärtusi märgitakse sageli väiketähtedega:

$ℓ = 0$ vastab $s$ ,
$ℓ = 1$ vastab $p$ ,
$ℓ = 2$ vastab $d$ ,
$ℓ = 3$ vastab $f$
jne.

Tähed on võetud naatriumi spektraalseeriate ingliskeelseist nimetusist: $s$ –sharp–terav, $p$ –principal–põhiline, $d$ –diffuse–hajus, $f$ –fundamental–peamine. Need seeriad on seotud vastavate kvantolekutega.

Seisundit, milles $n = 1$ , $ℓ = 0$ tähistatakse lühidalt $1 s$ , $n = 3$ , $ℓ = 2$ – $3 d$ jne

2.1.4 Elektroni spinn

Joon. 7.10. Spinni kajastatav vesiniku aatomi orbitaalmudel: elektronigi "aasta" jaguneb imelühikesteks "ööpäevadeks"

Kui aatomite spektreid uuriti eriti täpsete, suure lahutusvõimega aparaatidega, ilmnes, et paljud spektrijooned on lõhestunud kaheks lähestikku komponendiks, nad moodustavad dublette (lad. duplicare - kahestama). Et seda kahestumist seletada, tuli elektroni kvantseisundite kirjeldamiseks peale kvantarvude $n$ , $ℓ$ ja $m_{ℓ}$ võtta tarvitusele veel neljaski, mis siis, vastavalt joonte kahestumisele, võib omada ainult kahte väärtust: $+ 1 / 2$ ja $- 1 / 2$ . See kvantarv sai nimeks spinn (tähis - $s$ ).

Nimi tuleb sellest, et esialgu arvati, nagu võiks elektron peale orbiidil tiirlemise ka oma telje ümber pöörelda (ingl. to spin – pöörlema, ketrama) – justkui planeedidki (joon. 7.10). Kaks väärtust olnuks siis seotud kahtpidi – päri- ja vastupäeva pöörlemisega. Hiljem tuli küll välja, et see makroilmast laenatud kena võrdlus on mikroosakeste jaoks liig robustne, aga nimetus jäi. Õigem on kujutleda spinniga osakest imepisikese magnetina, mida iseloomustav suurus, magnetmoment, võib olla kahtpidi orienteeritud. Kvantfüüsikas tõdetakse, et spinn on mikroosakeste samasugune püsiomadus kui laengki. Mõnel osakeseliigil on ta ka täisarvuline, nt footoni spinn on $1$ . Rangelt ja järjekindlalt järeldub spinni olemasolu relativistlikust kvantmehaanikast, mille lainevõrrandi koostamisel on aluseks võetud A.Einsteini erirelatiivsusteooria. Sellest selgub ka, miks spinnkavantarvu väärtus peab olema just $1 / 2$ , nii erinevalt teistest, täisarvulistest kvantarvudest. Relativistliku kvantmehaanika lõi inglane Paul Dirac (l. pool diräkk; 1902–1984).

Spinnita ei seletuks ka paljud teised nähtused peale spektridublettide. Kui näiteks näete magnetrauda kirjaklambreid haaramas või kompassinõela põhja-lõuna suunda pöördumas, on siingi mängus spinn: ferromagnetism johtub raua-aatomi elektronide spinnist.

Niisiis

Elektroni kvantseisundi määravad kvantarvud

Niisiis määravad elektroni kvantseisundi aatomis lõplikult neli kvantarvu: $n$ , $ℓ$ , $m_{ℓ}$ ja $s$ .

Küsimused ja ülesanded

Kuidas peaks valemeid (7.8 – 7.14) teisendama, et nad oleksid rakendatavad vesinikusarnastele üheelektroonsetele ioonidele,nagu

H e^{+}

L i^{2 +}

B e^{3 +}

jne., mille tuumalaeng

Z > 1

answer

Vaata veelkord joonist 7.2. Kuidas pääseb elektron läbi leiulaine sõlmede naaberpaisudesse, kui sõlmedes on tema leiutõenäosus null?

answer

Millise energiaga footoneid kiirgaks kuubikusse küljepikkusega

L = 0, 1 n m

(võrdne vesinikuaatomi umbkaudse läbimõõduga) suletud elektron siirdel esimesest ergastatud seisundist põhiseisundisse, kui ta liikumissuund ristub kuubiku tahkudega.

answer

Milline energiaist on Bohri aatomimudelis absoluutväärtuselt suurim: kas koguenergia, kineetiline või potentsiaalne energia?

answer

Aatomi ionisatsioonienergia on

9 e V

. Leia põhiseisundi energia

E_{1}

answer

Leia vesiniku aatomi põhiseisundi raadius, kui aatomit ei hoiaks koos mitte elektrijõud, vaid gravitatsioonijõud.Analüüsi saadud tulemust, ms võrreldes seda Neptuuni (kaugeim planeet) orbiidi raadiusega, mis on

4, 5 \cdot 10^{12} m

answer

Stopp! Jäta meelde!

Leiulained ja seisulained

Joonlõigule pikkusega L sulustatud elektroni leiulained seiskuvad seisulaineteks pikkusega $λ = 2 L / n$ , $n = 1, 2, 3...$ .

Kvanditud kiirus ja energia

Vastavalt de Broglie seosele $λ = h / m v$ on kvanditud, s.o. hüppeliselt muutuv ka osakese kiirus ja energia; neid määrab kvantarv $n$ .

Kvantumite viisi

Energia jäävusest tingitult saab sulustatud elektron energiat omandada ja loovutada ainult kindlate kvantumite (kvantide) viisi, mis võrduvad lähte- ja lõpptasemete energia vahega.

Kolme dimensiooni sulustatud elektroni energiatasemed

Kolmemõõtmelisse ruumiossa sulustatud elektroni leiulained ja energiatasemed on määratud kolme kvantarvuga.

Ringorbiidil tuuma ümber tiirleva elektroni leiulained

Ringorbiidil tuuma ümber tiirleva elektroni leiulained peavad rahuldama seost $2 π r = n λ = n (h / m v)$ ehk $m v r = n ℏ$ . Sellest lähtub Bohri - de Broglie’ vesinikuaatomi mudel, milles aatomi energiatasemed määrab valem $E_{n} = - 13, 6 / n^{2} e V$ ja kiiratud või neelatud footonite energia võrdus $h f = E_{k} - E_{m}$ . Need valemid on heas kooskõlas katsega.

Kolmemõõtmelise aatomi elektroni seisulained

Kvantmehaanikas näidatakse Schrödingeri võrrandit lahendades, et kolmemõõtmelises aatomis määravad elektroni seisulainete kuju ja orientatsiooni kolm kvantarvu: peakvantarv $n = 1, 2, 3...$ , kõrval- e. orbitaalkvantarv $ℓ = 0, 1, 2... (n - 1)$ ja magnetkvantarv $m_{ℓ} = 0, \pm 1, \pm 2... \pm ℓ$ .

Elektroni energiatasemed vesinikuaatomis

Elektroni energiatasemed vesinikuaatomis sõltuvad peakvantarvust $n$ , mitmeelektroonses aatomis ka kõrvalkvantarvust $ℓ$ . Magnetkvantarvust sõltuvad energiatasemed ainult magnetväljas.

Algosakese spinn

Massi ja laengu kõrval on algosakesele püsivalt omane spinn, mis iseloomustab tema sise-magnetomadusi. Elektroni spinni ja tema orientatsiooni määrab spinnkvantarv $s = \pm 1 / 2$ .

Testi ennast!

2.2 Vesinikult heeliumile, heeliumilt liitiumile...

Siin saame teada

Milliseid seaduspärasusi järgivad elektronid aatomisse paigutudes.
Kuidas tekkiv süstemaatika paigatab elemendid perioodilisustabelisse.

2.2.1 Tõrjutusprintsiip

Joon. 8.1. Kirsid tuutusse, elektronid aatomisse ...

Eri elementide aatomeid eristab eeskätt laenguarv $Z$ : $Z$ prootonit tuumas ja sama arv elektrone selle ümber elektronkattes parvlemas. (Muidugi on enamikus tuumades ka mingi arv neutraalseid tuumaosakesi, neutroneid, kuid nendest ei sõltu, mis elemendile aatom kuulub ja aatomi omadusi mõjustavad nad nõrgalt.)

Kuidas need $Z$ elektroni tuuma ümber paiknevad? Positiivne tuum tõmbab neid kõiki endale võimalikult lähemale. Elektroni “koht” aatomis on tema leiulaine. Vesinikuaatomis määratlevad selle kvantarvud $n$ , $l$ , $m_{ℓ}$ ja $s$ . Tuumale lähima, põhiseisundi madalaimale energiatasemele vastava leiulaine $n = 1$ , edasi kihistuvad ergastatud kvantseisundid , mille $n = 2, 3$ jne. Oletame, et vesiniku leiulained ja kvantarvud kõlbavad alglähendina ka mitmeelektroonsete aatomite jaoks. Elementide spektrite ning füüsikaliste ja keemiliste omaduste uurimine näitab, et laias laastus on selline alglähend mõistlik. Kas, alludes tuuma tõmbele, asuvad kõik $Z$ elektroni (nt süsinikuaatomi $6$ , raua $26$ jne) tuumale lähimasse leiulainesse? Siis sarnaneks kõikide aatomite spektrid vesiniku spektrile. Spektrijoonte asend ainult nihkuks vastavalt tegurile $Z^{2}$ , mis tuleb energiatasemete avaldisse, kui $Z > 1$ . Ja kõigi elementide keemilised omadused oleks tõenäoselt üsna sarnased.

See ei vasta tegelikkusele. Miks? Et vastust saada, toome võrdluse tavaelust. Korjame kirsse koonilisse tuutusse (joon. 8.1). Esimene kirss langeb tuutu tiputeravikku, kus tema potentsiaalne energia Maa raskusväljas $m g H_{1}$ on minimaalne. Seda on siis ka koguenergia, kui ta tippu veerenult paigale jääb. Nii järgib kirss energia miinimumprintsiipi. Järgmine kirss aga jääb ülespoole ( $m g H_{2} > m g H_{1}$ ), sest eelmine on ees. Makromaailmas ei saa kaks eset olla ühtaegu samas kohas. Kas see aksioom, tõrjutusprintsiip, kehtib ka mikroosakestele? Selgub, et vähemalt elektronide puhul kehtib. Siin tuleb seda väljendada nii:

Samas aatomis ei saa olla kahte ühesuguste kvantarvudega ( $n$ , $ℓ$ , $m_{ℓ}$ ja $s$ ) elektroni.

Selle printsiibi sõnastas Šveitsi füüsik Wolfgang Pauli ja see on tuntud Pauli keeluprintsiibina (ehk tõrjutusprintsiibina).

Taas ilmneb mikromaailma näiv veidrus: Pauli printsiip kehtib ainult poolearvulise spinniga osakestele, fermionidele, nagu elektronid ( $s = \pm 1 / 2$ ). Ta ei kehti aga täisarvulise spinniga osakestele, bosonitele, nt footonitele, mille spinn on $1$ . Fermionideks ja bosoniteks jaotatakse osakesi itaallase Enrico Fermi (1901–1954) ja hindu Satiendranatah Bose’i (l. boos, 1894–1974) järgi, kes kumbki lõid teooriad kummastki klassist pärinevate osakeste kogumite kirjeldamiseks.

Energia miinimumprintsiip on õieti energia jäävusseaduse järeldus. Kui kehade või osakeste kogum (süsteem) väljastpoolt energiat juurde ei saa (isoleeritud süsteem) ja ta pole tasakaaluolekus, on tal energia jäävust eiramata ainus võimalus energiat ära anda, kuni loovutamine mõne seesmise tõkke taha jääb (nt kirss veereb tuutu põhja, elektron langeb põhitasemele).

2.2.2 Aatomite süstemaatika

Energia miinimumprintsiip koos Pauli printsiibiga tingivad aatomite elektronkatte kihilise, sibulataolise ehituse. Kihi numbriks (tuumast alates) on peakvantarv $n$ . Sageli tähistatakse kihte $n = 1, 2, 3, 4...$ suurtähtedega $K$ , $L$ , $M$ , $N$ ... (Tähistus pärineb elementidele iseloomuliku, karakteristliku röntgenikiirguse spektroskoopiast. Muide, ka laenguarv $Z$ on määratud kõige usaldusväärsemalt elementide röntgenispektrite kaudu.) Rehkendame Pauli printsiipi järgides, mitu elektroni ( $N_{n}$ ) mahub igasse kihti. Igal $n$ väärtusel $ℓ = 0, 1, 2 . . . (n - 1)$ , iga $ℓ$ väärtuse juures $m_{ℓ} = 0, \pm 1, \pm 2 . . . ℓ$ , ja iga $m_{ℓ}$ väärtuse juures võib veel spinn olla $\pm 1 / 2$ , seega kokku $2 ℓ + 1$ võimalust. Saame

\begin{matrix} N_{n} & = & 2 Σ (2 ℓ + 1) = & 2 (1 + 3 + 5 + 7 + \dots [2 (n - 1) + 1]) \end{matrix}

See on aritmeetiline rida, mille $k$ liikme summa

S_{k} = k \cdot \frac{a_{1} + a_{k}}{2}

( $a_{1}$ ja $a_{k}$ on rea alg- ja lõppliige); leiame, et

N_{n} = 2 n \cdot \frac{1 + (2 n - 1)}{2} = 2 n^{2}

ehk $K$ -kiht mahutab $2$ , $L$ - $8$ , $M$ - $18$ ... jne elektroni (vt.joon. 8.4 kus vakantsed kohad sisekihtides on tähistatud mullikestega). Konstrueerime nüüd elektronide kihistumisskeemi aatomitele $Z = 1, 2, . . .20$ ja paigutame skeemid perioodsussüsteemi lahtritesse (joon. 8.2). Rõhutame: ringid skeemidel pole tagasipöördumine planetaarmudeli orbiitide juurde, vaid visandavad üksnes elektronkihtide paiknemist tuuma suhtes ning elektronide arvu kihtides.

Joon. 8.2. Perioodsus süsteemi esimeste perioodide elementide aatomite elektronkatete lihtsustatud visandid (alakihte näitamata).

Neid skeeme vaadeldes taipame, kuidas elementide omaduste perioodiline kordumine Mendelejevi perioodsussüsteemis tuleneb aatomite ehitusest.

Elementide keemilised ja füüsikalised omadused sõltuvad elektronide arvust väliskihis.

See arv ühtib perioodsussüsteemi rühma numbriga, aga rühma kuuluvad sarnased elemendid. On ka loomulik, et just väliskiht, aatomi “koor” on kõige kergemini mõjutatav. Selles on tuumast kaugeimad, kõige nõrgemini seotud elektronid, valentselektronid. Nemad saavad aatomite lähenedes kokku teiste aatomite väliskihtidega, luues keemilisi sidemeid ja seeläbi molekule. Omaduste perioodilise korduvuse ilmeka näitena on joonisel 8.3 elementide ionisatsioonienergia sõltuvus laenguarvust.

Joon. 8.3. Aatomite ionisatsioonienergia sõltuvuses laenguarvust ilmneb selgesti perioodsus.

Joon. 8.2 uurides võib esialgu näida, et kaaliumi ja kaltsiumi skeemi on lipsanud viga: kuigi M-kiht on veel täitumata, selles on terveni $10$ “tühikut”, on lisandunud $19$ . elektron sattunud $N$ -kihti. Kuid teame, et kaalium on ühevalentne leelismetall, omadustelt sarnane liitiumi ja naatriumiga. Järelikult peaks tema väliskihis tõepoolest olema üksainus, ja mitte $9$ elektroni. Ka spektroskoopia kinnitab joonestatud skeemi õigsust. Seletus on selles, et mitmeelektroonse aatomi energiatasemeid hakkab tuntavalt mõjutama ka kvantarv $ℓ$ . (Vesinikuaatomis ilmnenud tasemete kidumine kõrvaldatakse). Oluliseks saavad elektronide vastastikused tõukejõud.

Kvantarvu $ℓ$ järgi lõhestuvad elektronkihid omakorda alakihtideks, nagu $1 s$ , $2 s$ , $2 p$ , $3 s$ , $3 p$ , $3 d$ ...... Joonisel 8.4 on alakihtide järjestus tuumast arvates, nagu see tuleb välja kvantmehaanilistest arvutustest. Muide, päris täpseid valemeid, nagu saadakse vesiniku aatomi jaoks, pole mitmeelektroonsetele aatomitele võimalik tuletada. Kuid kõigi aatomite kohta saab teha ligikaudseid arvutusi, mille tulemused langevad piisavalt hästi katseandmetega kokku.

Jooniselt 8.4 näeme, et alakiht 4s asetub tõesti tuumale lähemal kui $3 d$ ning omab siis ka madalamat energianivood, järelikult peabki enne hõivatama. (Argooniaatomis sai eelmine $3 p$ alanivoo täis.) Ka $Z$ edasisel kasvul tuleb korduvalt ette selliseid ristumisi, kus suurema n ja väiksema l-ga tase on allpool väiksema $n$ ja suurema $ℓ$ -ga tasemest ning täitub enne.

Mendelejevi tabeli põhjalikumal käsitlemisel põrkume veel reale teistelegi keerukustele. Nende lahendamine jääb juba süvendatud füüsika- ja keemiakursustesse.

Joon. 8.4. Aatomi elektronkihtide järjestus. Mullikesed esimestes kihtides sümboliseerivad vabu kohti täitmata alakihtides ja kihtides. Rooma number tähistab kihi ( $\equiv$ elementide süsteemi perioodi) numbrit, sulgudes suurim võimalik elektronide arv kihis. Paremal alakihtide tavapärane tähistus, ülaindeksis elektronide maksimaalarv; punase tähisega alakihid täituvad enne "normaalset" järjekorda.

Stopp! Jäta meelde!

Tõrjutusprintsiip

Tõrjutusprintsiip (Pauli keeld): ühes ja samas aatomis ei saa olla kaht elektroni, mille kõik 4 kvantarvu $n$ , $l$ , $m_{l}$ ja $s$ langeksid kokku.

Elektronid elektronkattes

Aatomi laenguarvu $Z$ suurenedes lisanduvad elektronid elektronkattesse nii, et nende energia oleks minimaalne ja tõrjutusprintsiip järgitud. Nii kujuneb kihiline elektronkate; kihi järjenumbriks (tuumast arvates) on peakvantarv $n$ , alakihi määrab kõrvalkvantarv $l$ . Ühte elektronkihti saab kuuluda maksimaalselt $2 n^{2}$ elektroni.

Elementide perioodilisussüsteem ja elektronkihid

Elementide perioodsussüsteem peegeldab aatomite elektronkatete kihistumist. Piki perioodsustabeli iga rida (perioodi) on $Z$ kasvu järjekorras reastatud elemendid, millede aatomeis järjest täitub sama, reale vastav elektronkiht. Tulpades on sarnaste omadustega elemendid, mille aatomite välises elektronkihis on võrdne arv elektrone.

Kontrollküsimused

Kuidas peaksid elektronid paigutuma elektronkihtidele räni aatomis? Kontrolli oma vastust joonisel 8.2.

answer

Mis on aatomite ionisatsioonienergia? Kas aatomite sisekihi elektroni ionisatsioonienergia on suurem või väiksem kui väliskihi elektroni ionisatsioonienergia?

answer

Millistena tuleks joonistada aatomi elektronkatteid kui elektronid oleksid bosonid?

answer

Tooge veel mõni näide tõrjutusprintsiibiga sarnastest piirangutest igapäevaelus.

answer

Mitu elektroni peaks mahtuma

N

-kihti? Kontrolli oma hinnangut, kasutates internetiallikaid.

answer

Mis võiks olla põhjuseks, et elementide laenguarv on määratud justnimelt röntgenkiirgust kasutades?

answer

Testi ennast!

3 Aatomikooslused – molekulid ja kristallid

3.1 Aatomitelt molekulidele ja kristallidele

Siin saame teada

Kuidas moodustuvad keemilised sidemed.
Missugune jõud hoiab enamusi aineid koos.
Kuidas moodustuvad kristallid ja kuidas käituvad kristallides elektronid.

3.1.1 Keemiline side: elektronide 'annetamine' ja 'ühistamine'

Kõik me tunneme keedusoola $N a C l$ . Miks kaks nõnda erineva lihtaine – metalli ja gaasi aatomit moodustavad keemilise sideme, püsiva ühenduse $N a C l$ molekulis?

Nii $N a$ kui ka $C l$ aatomid muutuvad suhteliselt kergesti $N a^{+}$ positiivseteks ja $C l^{-}$ negatiivseteks ioonideks. Kui nüüd $N a$ ja $C l$ aatomid satuvad lähestikku, “kingib” $N a$ oma väliselektroni $C l$ -le. Positiivsete ja negatiivsete ioonide vahel tekib tõmme, mis nad seostabki ioonsidemesse.

Samaviisi tekivad teised leelishalogeniidid $N a B r$ , $K B r$ , $K C l$ , $R b I$ , $L i F$ jt. Ühend $M g O$ tekib kahe elektroni siirdel magneesiumilt hapnikule, nii et moodustuvad ioonid $M g^{2 +}$ ja $O^{2 -}$ . $N a_{2} S$ kujuneb kahest $N a^{+}$ ja ühest $S^{2 -}$ -ioonist.

Miks loobub $N a$ nii kergesti oma ainsast väliselektronist, $C l$ seevastu ei “raatsi” ära anda ühtki oma seitsmest, kuigi need asuvad samas $M$ -kihis kui naatriumilgi? Jooniselt 9.2 näeme, et $N a$ -aatomis varjestavad tuumalaengut $+ 11 e$ valentselektroni eest $10$ $K$ - ja $L$ -elektroni kogulaenguga $- 10 e$ . Väliselektroni jääb tuuma poole tõmbama vaid ainus tasandamata laeng $+ 1 e$ . Seevastu $C l$ tuumalaeng on $+ 17 e$ , $10$ siseelektroni suudavad kompenseerida nendest $+ 10 e$ , igaüht seitsmest väliselektronist jääb siduma $7$ korda suurem efektiivne tuumalaeng kui $N a$ aatomis.

Joon. 9.2. Kloori iga väliselektron on seotud hoopis tugevamini kui naatriumi oma.

Siiski, joon. 8.3 näitab, et $C l$ ionisatsioonienergia pole mitte $7$ , vaid vaevu $3$ korda suurem kui $N a$ -l – kõik ei seletu algelise aritmeetikaga.

Vesinikugaasis on $H$ -aatom molekulidena $H_{2}$ .

Siin ei liitu aatomid ioonidena, sest $H$ -aatom saab oma ainsat elektroni vaid loovutada, muutudes positiivseks iooniks. $H_{2}$ moodustamisel ühistatakse kummagi aatomi $2$ elektroni, nad asetuvad ühisesse leiulainesse $2$ prootoni ümber.

Joon. 9.3. Vesiniku aatomeist saab molekul: A – eemaldatud aatomid; B – ühtpidi spinnid, ühinemine keelatud; C – eripidi spinnid, ühinemine lubatud, elektronpilved valgustavad ühte; elektroni leiutõenäosus on suurim tuumade vahel, kuhu elektrone tõmbavad mõlemad tuumad; D – klassikaline näitpilt kahe tuuma ümber orbiitlevaist elektronidest.

Tõrjutusprintsiibist tingituna on eeltingimuseks muidugi kummagi elektroni spinni vastassuunalisus (üks peab “pöörlema” päri-, teine vastupäeva). Ühinevate aatomite tuumade tõuge tasakaalustatakse sedaviisi, et elektronpilve tihedus (leiulaine intensiivsus) on suurim tuumade vahelises alas. Sellist sidet nimetatakse kovalentseks ehk homeopolaarseks. Tema moodustumisel ühistatakse ikka vastasspinnidega elektronpaarid, üks elektron kummaltki ühinevalt aatomilt. (Joon 9.4 on mõnede molekulide kuulmudelid. Kuigi ioonsidemega ühendeid on üsna palju, on homeopolaarse sidemega ainete hulk looduses siiski valdav.

Joon. 9.4. Molekulimudeleid. Aatomid jäävad molekulis püsima asendeisse, milles molekuli potentsiaalne energia on väikseim.

Mõnede ühendite puhul on õigem sidet käsitada ioonse ja kovalentse sideme seguna, justkui veedaks ühinenud aatomid osa aega ioonidena, osaks ajaks aga ühistaks elektronid. On veel rida keerukamaid keemilise sideme liike.

3.1.2 Molekulidelt kristallidele

Kui keedusoola lahuses on hulgiti $N a^{+}$ ja $C l^{-}$ - ioone (üleküllastatud lahus), on suur tõenäosus ioonide kohtumiseks ja järjest uute keemiliste sidemete tekkeks. Hakkab kasvama $N a C l$ kristall (joon.9.5).


Joon. 9.5. $N a C l$ kristalli tekkimine.	Joon. 9.6. Nõnda kasvatatakse kristalle.Elektriahjus asetsevasse tiiglisse p annakse kristalliseeritav aine, mis kõrgkuumuses (nt. rubiini jaoks $2050^{\circ} C$ ) sulab. Sulandisse lastakse jahutatava varda otsas idukristallike, mille külge kasvavat jääpurikasarnast monokristalli tõstab elektriajam aegamööda sulandist välja.

Olemuselt on see supermolekul, milles on hiidhulk koostisaatomeid või -ioone. Samuti võib jääpurikat meenutav suur monokristall hakata kasvama kõrgtemperatuuril sulatatud ainesse ( $N a C l$ , aga ka nt $G e$ , $S i$ jne) lastud jahutatava idukristalli külge (joon. 9.6).

Kristallides on aatomid/ioonid paigutatud kindlas korras, nad moodustavad ruumvõre (joon.9.7).

Joon. 9.7. Keedusoola kristalli kuulmudelid. Igat Na⁺ iooni ümbritseb 6 Cl^- iooni ja vastupidi. See tagab ioonide tugevama seotuse kristallis, võrreldes üksikmolekulidega.

Nagu elektroni laineomadustest, nii ka kristallide mikrostruktuurist annavad veenvat tunnistust difraktsioonikatsed. Sõltub ju difraktsioon nii difrageeruvate lainete pikkusest kui ka võrekonstandist. Kui lainepikkus on teada, saab määrata võrekonstanti. Kristallides on aatomid paigutatud väga tihedalt, võrekonstant on vaid $10^{- 10} m$ ( $0, 1 n m$ ) suurusjärgus. Seepärast tuleb kristallide difraktsioon-uuringuiks kasutada hästi lühikesi laineid: röntgenikiirgust, elektronide või neutronite kimpe (vt.joon.4.2). Ainult siis on difrageerunud kimpude hälbed piisavad, et difraktsioonipilte eristatada ja tõlgendada. Tänapäeval teevad tunnelmikroskoobid kristallivõre lausa silmnähtavaks.

Ruumvõresse korrastuvad aatomid seepärast, et sellises paigutuses osutub nende kogumi potentsiaalne energia minimaalseks (meenuta tuutumudelit, kirsside kogunemist tuutu põhja).

Siiski kirjeldab ruumvõrepilt kristalli mikroehitust vaid üldjoontes, ta on idealiseering, lihtsustus, nõnda kui teisedki füüsikas pruugitavad mudelid. Tegelikes kristallides esineb alati hälbeid võre ideaalsest korrapärast – kristallivõre mikrodefekte, lühidalt võredefekte. Nendeks võivad olla lisandid (nt. üksikud $K^{+}$ -ioonid, mis asendavad $N a^{+}$ -ioone $N a C l$ võres), tühjaks jäänud võresõlmed – vakantsid, või siis võresõlmedest irdunud aatomid/ioonid. Võredefektid, eeskätt lisandid, mõjutavad oluliselt tahkiste elektrilisi, optilisi jpt. omadusi. Seepärast kuulub lisandamine e. legeerimine (lad. ligare – siduma, ühendama) paljude materjalide valmistamiskäiku. Sageli piisab juba tühistest lisandihulkadest ( $10^{- 2} . . . 10^{- 6}$ ) aine omaduste tunduvaks teisendamiseks. Nt. muutmaks terast roostevabaks, lisatakse talle kroomi ja niklit. Legeeritakse pooljuhtmaterjale, helendusaineid – luminofoore, laserikristalle jne. Tahkisefüüsikas on kombeks märkida lisandeid põhiaine keemilise valemi lõppu, kooloni järele, nt. $Z n S : C u$ .

Kristallid on tahkete ainete levinud olelusvorm. Harva leidub küll ehedalt suuri monokristalle, aga paljud ained ja objektid on müriaadide pisikeste kristallikeste liidendid: nad on polükristalsed (kr. k. monos – ainus, poly – palju). Looduslike monokristallide näiteks on vääriskivid, polükristalsed on metallid, kivimid, liivakübemed, põhiosa tervest maakoorest .

Metallide kristallides on kristallivõreks seostunud positiivsed ioonid. “Sideaineks”, mis vastastikku tõukuvaid ioone tugevasti kristalliks seob, on nende aatomite väliskihtidelt kristalliseerumisel vabanenud elektronid, “elektrongaas”, milles elektronid võivad peaaegu vabalt liigelda ioonide vahel. (Nende elektronide leiulaine hõlmab kogu kristalli. Ta sarnaneb vaba elektroni sinusoidaalse leiulainega, ainult on moduleeritud, st. tema amplituud on suurem ioonide vahetus läheduses ja väiksem neist eemaldudes). Seepärast ongi metallid head elektrijuhid. Isolaatoreis nagu teemant, kvarts, tefloon jt. jäävad elektronid seotuiks oma aatomitega, pole vabu voolukandajaid. Lõppeks pooljuhtides, mis on nime saanud sellest, et nende elektrijuhtivus on isolaatorite ja metallide vahepealne, on ainult osa aatomeid ioniseerunud ja loovutanud elektronid kristalli ühisesse leiulainesse.

Küsimused ja ülesanded

Miks joon. 4.2 toodud röntegenikiirte difraktsioonipildil kristallivõrelt on täpid, mitte triibud? Vihje: Milline peaks tulema difraktsioonipilt, kui asetada kaks tasast difraktsioonivõret üksteisele, nii et pilud on risti?

answer

Miks puruneb keedusoola krstall haamrilöögist mitmesuguse suurusega tükikesteks, mis alati on risttahukakujulised?

answer

Stopp! Jäta meelde!

Aatomitest molekulide ja kristallideni

Aatomeid seob molekulideks ja kristallideks keemiline side, mille põhiliigid on ioon- ja kovalentside.

Ioonside ja kovalentside

Ioonside tekib positiivsete ja negatiivsete ioonide vahel, kovalentside – elektronpaaride ühistamisel.

Kristallid

Kristallid on makroskoopilised hiidmolekulid, milles aatomid või ioonid on paigutunud korrapärasesse (perioodiliselt korduvate ühikrakkudega) ruumvõresse.

Testi ennast!

3.2 Metallid, pooljuhid ja dielektrikud

Siin saame teada

Mis on energiatsoonid ja kuidas need mõjutavad materjalide elektrilisi omadusi.
Kuidas on võimalik kristallide elektrijuhtivust tõsta.

3.2.1 Kristallide energiavöötmed – tsoonid

Kuna kristallis on aatomid tihedasti koos, mõjutavad nad üksteist tugevasti. Oodatavasti teiseneb siis ka energiatasemete pilt vabade aatomitega võrreldes. Spektrite, elektriliste jpt. omaduste uurimine kinnitab seda oletust. Elektronkatte sisekihtide elektronide energiatasemed jäävad kristallis peagu muutumata, kuid väliselektronide tasemed paisutab aatomite elektriline vastastikmõju laiadeks, mitme elektronvoldi laiusteks energiavöötmeteks e. energiatsoonideks (joon 10.1).

Joon. 10.1. Energiatasemete teisenemine energiavööndeiks – tsoonideks aatomite liitumisel kristalliks; $P$ – aatomi põhitase, $E$ – põhitasemele järgnev ergastustase, $Δ E$ – keelutsoon ehk keelupilu.

Kui kristalliks on ühinenud $N$ aatomit, hargneb iga tase tsoonis $N$ alatasemeks. Kuidas hõivatakse alatasemed tsoonides elektronidega? Kehtima jääb endiselt energia miinimumprintsiip koos Pauli tõrjutusprintsiibiga.Joonisel 10.1 on visandatud 6 aatomi energiatasemete hargnemine tsooniks. Pilt jääb sarnaseks, kui mõttes järjest suurendame ühinevate aatomite arvu. Kuigi alatasemete energeetiline vahekaugus on ääretult väike, jäävad täitumisprintsiibid jõusse.

Juhul A on aatomi kõrgeimal hõivatud tasemel ainult üks elektron (nagu nt liitiumis). Kuna tõrjutusprintsiip lubab tsooni igale alatasemele asuda kahel vastasuunaliste spinnidega elektronil, jääb kõrgeim hõivatud tsoon pooleni täidetuks. (Osaliselt hõivatud tsoonid võivad tekkida ka tsoonide osalisel kattumisel kristalliseerumise käigus.) See on metalli juhtum. Pooltäidetud tsooni elektronid ongi liikumisvõimeline elektrongaas metallides.

Juhul B on aga aatomite kõrgeimal hõivatud tasemel kaks (muidugi vastasspinnidega) elektroni. Selline on olukord mittemetallides. Nüüd täidetakse kristallis kõrgeim hõivatud tsoon “pilgeni”. Nõnda kujunevad dielektrikud ja pooljuhid.

Joon. 10.2 Energiatsoonid metallides, pooljuhtides ja dielektrikutes. Võimalikke ja võimatuid siirdeid tähistavad nooled selgitavad miks metallid ja pooljuhid neelavad valgust, dielektrikud aga on läbipaistvad.

Elektronide laineomaduste tõttu ei saa nad omandada energiaid, mis jäävad pilusse $Δ E$ täidetud ja tühja tsooni vahel. Seepärast nimetatakse seda vahemikku keelutsooniks. Kuna hõivatud tsoon täitub kristalliaatomite väliskatte elektronide e. valentselektronidega, nimetatakse seda valentsitsooniks. Keelutsoonile järgnev täitmata tsoon kannab juhtivustsooni nime. Järgnevas alalõigus selgub, miks.

Pooljuhte eristab dielektrikutest keelutsooni laius. Kui see tsoon on suhteliselt kitsas ( $Δ E \sim 1 e V$ ), on tegemist pooljuhiga, laia keelutsooni (suurusjärgus $5 - 10 e V$ ) puhul – dielektrikuga.

3.2.2 Kristallid elektriväljas – elektrivool kristallides; elektronid ja augud

Elektriõpetusest teame, et elektrivool on laengukandajte suunatud liikumine. Tahkistes on laengukandjateks elektronid (mõned erandid, nn. tahked elektrolüüdid, välja arvatud). Suunatud liikumisse tõukab laengukandjaid elektrijõud, mis neile mõjub tahkisele rakendatud elektriväljas. See jõud kiirendab elektrone, lisades neile kineetilist energiat. “Pakutavat” energiat saavad elektronid vastu võtta ainult siirete kaudu vabadele kõrgematele energiatasemetele, nt. tsooni asustamata alatasemetele. Vaatame, millised on selleks võimalused metallides, dielektrikutes ja pooljuhtides.

Metalli pooltäidetud tsoonis (see on ühtaegu nii valentsi- kui ka juhtivustsooniks) on külluses nii elektrone (elektrongaas!) kui ka vabu alatasemeid – energia kasvuruumi. Seepärast ongi nad suurepärased elektrijuhid.

Dielektriku tühjas juhtivustsoonis on “energiaruumi” avarasti, kuid seal puuduvad elektronid, mida väli võiks liikuma suunata. Valentsitsoonis on küll kõik alatasemed elektronidega täidetud, kuid väli ei saa neid kiirendada: puuduvad vabad alatasemed, millele elektrone kergitada (nagu tihedas rahvasummas: rõhutakse peale, aga liikuda pole kuhugi...). Nõnda ei juhigi nad voolu, on isolaatorid.

Et pooljuhi keelutsoon on suhteliselt kitsas, saab mõningane osa valentsitsooni elektronidest kristallivõre soojusvõnkumistelt küllalt energiat, et hüpata üle keelutsooni juhtivustsooni. Kuna seal on rohkesti vabu alatasemeid, saab väli neid kiirendada ja tekitada elektrivoolu. Sellest siis nimigi – juhtivustsoon. Elektronide hüppeid üle keelutsooni võib käsitada ka kui kristalliaatomite soojuslikku ioniseerimist, valentssidemete lõhkumist. Pooljuhi juhtivustsooni pääseb palju vähem elektrone, võrreldes metalli pooltäidetud tsooni “asukate” arvuga. Seetõttu jääbki pooljuhtide elektrijuhtivus tugevasti maha metallide omast (olenevalt ainest ja valmistusviisist langeb nende eritakistus vahemikku $10^{- 6} . . . 10^{8} Ω \cdot m$ metallide $10^{- 8} . . . 10^{- 7} Ω \cdot m$ vastu). Siit nimetuski – pooljuhid.

Joon. 10.3. Augu hüpakliikumine – järjestikused kaadrid.

Kuna pooljuhis on osa elektrone siiratud valentsitsoonist juhtivustsooni, jääb nüüd ka sinna vabu alatasemeid – “auke”. Täites neid auke, pääsevad ka valentsitsooni elektronid liikuma. Elektronjuhtivusele läbi juhtivustsooni lisandub aukjuhtivus valentsitsooni kaudu. Seda on hõlpsaim kujutleda pooljuhi aatomi ioniseerimisel tekkiva positiivse iooni näiva liikumisena läbi kristalli (joon.10.3): ioniseeritud aatom haarab kaotatud elektroni asemele naabri oma, see “röövib” omakorda järgmist ja nõnda muudkui aatomite ahelikku pidi edasi. Seega on siis auk positiivne laengukandja, ta triivib vooluallika negatiivse pooluse poole. Koguvool liitub elektronide ja aukude vastasuunalistest voogudest.

Pakume võrdluse argielust. Teatrisaalis on üksikuid tühje kohti. Vastutulelikud teatrilised loovutavad need hilinejaile, ise järjest kohalt-kohale ümber istudes. “Augud” liiguvad siis hilinejate poole vastu ümberistumiste suunda. Kui hilineja temani jõudnud kohale istub, modelleerib see rekombinatsiooni, elektroni ja augu taasühinemist, millest tuleb veel juttu.

Mida kõrgem on pooljuhi temperatuur, seda enam elektrone paisatakse juhtivustsooni ja rohkem auke jääb valentsitsooni. Juhtivus kasvab soojenedes järsult (eksponentsiaalselt), ja pooljuhte saab kasutada tundlike temperatuuritajurite – termotakistite ehk termistoridena. Metallides on asi vastupidi: soojenedes takistus kasvab: voolukandjate hulk seal ei muutu, sageneb nende hajumine võrevõnkumistel. Pooljuhtides korvab voolukandjate soojuslik rohkenemine paljukordselt takistuse termilise kasvu.

Täiendavaid voolukandjaid vabastab pooljuhis ka tema valgustamine, kui vaid footonite energia ületab keelutsooni laiuse (keskmine nool joonisel 10.2). See on sisefotoefekt ehk fotojuhtivus, mida rakendatakse valgustajurites – fototakistites.

3.2.3 Valguse neeldumine ja soojuse levik tahkistes

Tsoonipildist (joon 10.2) saame aimu ka tahkiste mõnedest teistest omadustest peale elektriliste, nt nende optilistest ja soojuslikest näitajaist. Teades, et nähtava valguse lainepikkus on vahemikus $400 - 700 n m$ ja footoni energia vastavalt $3, 1 - 1, 8 e V$ , võime mõista, miks metallid ja pooljuhid neelavad tugevasti valgust, on läbipaistmatud, isolaatorid (nt keedusool, teemant, kvarts, korund jt) aga läbipaistvad. Tõepoolest, energiat $2 - 3 e V$ saab hõlpsasti kulutada siireteks metalli pooltühjas juhtivustsoonis täidetud tasemeilt täitmata nivoodele. Sellest piisab ka pooljuhi $\sim 1 e V$ laiuse keelutsooni ületamiseks, jääb aga tublist vajaka isolaatori $5 - 10$ elektronvoldise keelutsooni ületamiseks (vt nooled joonisel 10.2). Neelata saab aine ju üksnes neid footoneid, mis ajendavad võimalikke siirdeid lubatud energiatasemete vahel.

Edasi, metallide vabad elektronid pole mitte ainult voolukandjad, vaid ka tõhusad soojusenergia edasitoimetajad. Isolaatoreis nad puuduvad. Seepärast ongi head elektrijuhid ka head soojusjuhid, kuid elektriisolaatorid ühtlasi soojusisolaatorid.

3.2.4 Lisandjuhtivus, doonorid ja aktseptorid

Pooljuhi juhtivust saab tunduvalt tõsta, viies kristalli selle kasvatamise käigus väheke (mõni miljondikosa) sobivaid lisandeid. Kui näiteks neljavalentse germaaniumi (neli väliselektroni) kristalli kasvatada viievalentse arseeni aatomeid, jääb üks elektron keemiliste sidemete moodustamisel ülearuseks ja vabaneb juhtivuselektronina (joon.10.4). Niiviisi saadakse valdavalt elektronjuhtivusega pooljuht – n-pooljuht (n – sõnast negatiivne, vihjamaks elektroni laengule). Elektrone loovutav lisand on doonor (ld. donare -annetama; vrdl. vereandja).

Joon.10.4. n- ja p-pooljuhi võrepilt (A) ja tsooniskeem (B). Üksikute lisandiaatomite tasemed ei teisene tsoonideks. +4 – põhiaine (Si, Ge) 4 valentelektroniga aatomid, +5 – doonorlisandid (As, Sb, Bi) 5-valentsed aatomid, +3 – aktseptorlisandid (Al, B, In, Ga) 3-valentsed aatomid.

Kui pooljuht sisaldab lisandit, millel on üks väliselektron vähem kui põhiaine aatomeil, saame valdavalt aukjuhtivusega pooljuhi, p-pooljuhi (p - positiivne). Vastav lisand on siis aktseptor (ld acceptor - vastuvõtja).

Aktseptor omastab põhiaine naaberaatomilt elektroni, jättes selle elektronkattesse augu, mis siirdub soojusliikumise toimel valentsitsooni (joon.10.4).

Joon 10.5. Omajuhtivusega pooljuhis (n & p) kannavad voolu nii elektronid kui ka augud, n-pooljuhis – peamiselt elektronid, p-pooljuhis – peamiselt augud; l – leppeline voolusuund.

Küsimused ja ülesanded

Joonisel 10.2 toodud tsoonipildid kehtivad rangelt võttes ainult absoluutse nulltemperatuuri juures (mis on muide saavutamatu). Joonista tsooniskeemid, mis kajastaksid olukorda toatemperatuuril.

answer

Muide, väga madalatel, absoluutsele nullile lähedastell temperatuuridel kaob erinevus pooljuhi ja dielektriku vahel. (Miks? – Vihje: kujutle kitsast ja laia kraavi.)

answer

Stopp! Jäta meelde!

Energiatsoonid kristallides

Kristallides (tahkistes) muunduvad aatomite/ioonide väliselektronide energiatasemed mitme $e V$ laiusteks energiatsoonideks, mille hõivamine elektronide poolt järgib tõrjutusprintsiipi ja mis on ühised kogu kristallile.

Energiatsoonid metallides

Metallides on kõrgeim energiatsoon ainult osaliselt elektronidest hõivatud. Seetõttu on nad head elektrijuhid: elektronid saavad tsooni hõivamata ossa tõustes ammutada elektriväljalt energiat ja liikuda.

Energiatsoonid isolaatorites

Isolaatoreis (dielektrikuis) ning tugevasti külmutatud pooljuhtides on kõrgeim hõivatud energiatsoon – valentsitsoon elektronidega täidetud. Liikumisvabadus puudub, elektrivool ei pääse läbi.

Laengukandjad pooljuhtides

Tavatemperatuuridel ergastab soojusliikumine pooljuhtides elektrone üle kitsa ( $\sim 1 e V$ ) keelutsooni kõrgemasse tsooni – juhtivustsooni, jättes valentsitsooni tühikuid – auke. Auk käitub elektriväljas nagu positiivse laenguga voolukandja. Pooljuhti läbiv vool vool liitub elektronide ja aukude voogudest.

Keelutsoon isolaatorites

Isolaatorites (dielektrikutes) on keelutsoon lai ( $5 - 10 e V$ ), soojusenergiast ei piisa juhtivuselektronide tekitamiseks.

Doonorlisandiga pooljuhtide elektrijuhtivus

Pooljuhtide ( $S i$ , $G e$ jt) elektrijuhtivust tõstavad lisandid – nii elektrone hõlpsasti loovutavad doonorid kui ka elektrone haaravad ning valentsitsooni auke jätvad aktseptorid. Doonorlisandiga (valdavalt elektronjuhtivusega) pooljuht on n-pooljuht, aktseptorlisandiga (vald

Testi ennast!

3.3 Pooljuhtelektroonika: diood, transistor, kiip

Siin saame teada

Milline on pooljuhtelektroonika tööpõhimõte.
Kuidas töötab transistor, kuidas töötab kiip.

3.3.1 Kihtstruktuurid. Diood

Pooljuhid said tõeliseks tehnika eldoraadoks, kui õpiti tegema neist kihilise piruka taolisi struktuure.

Joon. 11.1. Pooljuhtdioodi läbilõige (l – isolaator, K – hermeetiline kest, P – pn-siirdega pooljuhtkristall) ja tingmärk (nool näitab pärivoolu suunda)

Sulandades ühte plaadikese n-pooljuhist plaadikesega p-pooljuhist, saame kahekihilise pooljuhi. Nende ühinemiskiht on pn-siire. Jootnud kummagi poolme külge veel ühendusjuhtme, ongi valminud pooljuhtdiood (joon.11.1), mis toimib elektrivoolule ventiilina: ühes suunas juhib voolu hästi, teises peaaegu üldse mitte (vrd. rattakummi ventiiliga või ainult ühtpidi ringleva pöörduksega).

Kuidas alaldav tõkkekiht tekib? Asi algab sellest, et p-poolmes on rohkesti auke, n-poolmes – elektrone. Voolukandjate tiheduste erinevus hakkab läbi siirde tasanduma: augud valguvad (difundeeruvad) n-poolmesse, elektronid – p-poolmesse. Siirdealas jäävad n-poolmesse positiivsed doonoriioonid, p-poolmesse negatiivsed aktseptoriioonid (joon.11.2). Nende laengut ei tasakaalusta enam lahkunud elektronid ega augud. Selle kaksikihi elektriväli hakkab ülevalguvaid voolukandjaid tagasi tõrjuma, kuni tekib tasakaaluseisund.


Joon. 11.2. Potentsiaaliastangu (tõkkekihi)kujunemine pn-siirdel: e^- – p-poolmesse valgunud elektronid, e⁺ – n-poolmesse valgunud augud, A^- – kompenseerimata laenguga aktseptor- ja D⁺ – doonorlisandid.	Joon. 11.3. Pooljuhtdiood juhib voolu vaid ühes, pärisuunas.

Välise vooluallikaga saab tekkinud potentsiaaliastangut langetada või tõsta. Kui dioodile rakendada päripinge, s.o vooluallika positiivne poolus ühendada p-poolmega (joon.11.3), töötab väline elektrijõud kaksikkihile vastu ja dioodi läbib vool, mis pinge tõustes kiiresti kasvab (joon. 11.4). Pooluste vahetamisel (vastupinge), tugevdab väline väli sisemist tõkkevälja, ja vool kahaneb nulli lähedale (joon.11.3, 11.4). Kui diood lülitada vahelduvvooluringi, hakkab ta alaldama, vahelduvvoolust saab pulseeriv, tõukeline, kuid ühesuunaline vool. Voolutõukeid saab tasandada alaldiga rööbiti ühendatud kondensaatoriga (joon. 11.4).

Joon. 11.4. Pooljuhtdioodi volt-amperkõver (tunnusjoon) ja alaladustoime (punktiir – kondensaatori abil silutud alaldatud vool; nõrka vastuvoolu tingib omajuhtivus).

Alaldeid vajatakse tihti. Elektrienergiat on ökonoomne üle kanda vahelduvooluna, aga paljud seadised (sh. raadiod, televiisorid, arvutid jpt.) vajavad toiteks alalispinget. Samuti on alaldeid tarvis raadio teel edastatud heli-, video- ja teabesignaalide dešifreerimiseks (s.o. detekteerimiseks).

Peale alaldite on veel mitmeid eriotstarbelisi pooljuhtdioode. Kõigepealt optikakursusest tuttavad ventiilfotoelemendid, sh. päikesepatareid.

Edasi, kui teatavaist pooljuhtühendeist ( $G a A s$ , $G a P$ jt) valmistatud dioode, – valgusdioode – läbib pärivool, hakkavad need valgust kiirgama: siirdealas kohtuvad elektronid ja augud – rekombineeruvad (meenutame hilineja istumist teatris talle vastu liikunud kohale). Vabanenud energia läheb kiirguvaile footoneile. Valgusdioodid leiavad tööd indikaatoreina elektroonikaseadmeis, tekstide või numbrite kuvamiseks jm. Ka pooljuhtlaserid on olemuselt valgusdioodid. Nendest lähemalt edaspidi.

Transistori leiutasid 1948 USA füüsikud John Bardeen (1908–1991), Walter Brattain (1902–1987) ja William Shockley (1910–1989)

3.3.2 Dioodilt transistorile

Kui kaks pn-siiret luuakse vastasjärjestuses (nt np ja pn) ühisesse kristallipalasse, saadakse transistor, nüüdiselektroonika põhiline ehituskivi. Transistor oleks nagu kahe dioodi ühend, kusjuures dioodidel on ühine p-poole (npn-transistoris) või n-poole (pnp-transistoris, vt. joon.11.5).

Joon. 11.5. npn- ja pnp-transistori läbilõige ja tingmärk kummagi transistorvõimendusastme lülitusvisandil.

Seega on ta juba kolmekihiline pooljuhtstruktuur. Joonisel on märgitud transistorikihtide tavapärased nimetused: emitter (ld. emittere – välja saatma), kollektor (ld. collector – koguja) ja baas (ld. basis – alus; see nimetus on ilmselt jäänuk transistori algaegadest. ) Nimetus tuleneb ingl. sõnadest to transfer – üle kandma, siirdama, ja resistor – takisti. “Takistuse ülekanne” tähendab seda, et ühele siirdele rakendatud signaalipingega saab reguleerida, tüürida teise siirde takistust ja seeläbi ka väljundpinget. Transistor on aktiivseadis, mis võimendab elektrisignaale, teeb ümberlülitamisi, genereerib elektrivõnkumisi jpmt.

Transistoritest saab koostada väga erineva otstarbega lülitusi. Muuhulgas võib kaks transistorit ühendada bistabiilsesse, so kahe tasakaaluseisundiga lülitusse: üks transistor juhib, teine mitte, kusjuures sisendsignaal võib nende olekut vahetada. Selline lülitus on elektronarvuti põhielement: üks seisund modelleerib kahendsüsteemi arvu 1, teine – arvu 0.

Nii dioodide kui ka transistorite kasutatavaimaks materjaliks oli varem germaanium, praegu räni. Üha rohkem tehakse neid ka galliumarseniidist ja teistest pooljuhtühenditest.

Vaatame npn-transistori toimimist võimendusastmes. (pnp-transistor funktsioneerib samuti, ainult toiteallika polaarsus ja voolukandjate märgid on vahetatud.) Transistor eelpingestatakse nii (joon.11.2), et emitteri ja baasi vaheline siire (siire EB) saab päripinge, siire baas-kollektor (BK) aga vastupinge. Esimene on siis väikese, teine suure takistusega. Oluline nipp on selles, et baasikiht tehakse hästi õhuke (mõni μm). Päripinge mõjul emitterist baasi suunduvad elektronid valguvad peaaegu kõik õhukesest baasist läbi. Jõudes kollektorisiirdesse, vähendavad lisandunud voolukandjad selle takistust.

Joon. 11.6. npn-transistori lülitusviis ja võimendustoime. U_s, R_s ja U_v, R_v – vastavalt sisend- ja väljundpinge ning -takisti.

Joonis 11.6 näitab ilmekalt transistori võimendusefekti. Graafikul on taas pn-siirde tunnusjoon. Parem (varjutatud) pool vastab päripingestatud siirdele (dioodile) EB, vasak – vastupingestatud siirdele BK. Väike signaalipinge muutus ΔU_EB tekitab voolumuutuse ΔI_E. See kandub kärmesti läbi õhukese baasi peaaegu muutumata suuruses (ΔI_K ≈ ΔI_E ) üle siirdele BK. Et aga viimane on vastupingestatud, on vastav pingelangu muutus BK-siirdel DU_BK oluliselt suurem: ΔU_BK>> ΔU_EB. Sedasi toimibki transistor pingevõimendina, samuti võimsusvõimendina, sest ka võimsuskasvik

ΔI_K· ΔU_BK>> ΔI_E· ΔU_EB. Transistorite tüüpilised võimendustegurid on suurusjärgus mõnest kümnest mõne sajani.

Mõni sõna ka veidi teise tööprintsiibiga väljatransistorist ehk unipolaartransistorist (joon.11.7). Nende tarbimine laieneb praegu tormiliselt, eriti kiipide (jrgm. p.) koostises. Siin tüüritakse klemmide “läte” ja “suue” vahelist voolu homogeenses, siireteta pooljuhis. Tüürib isoleeritud elektroodile “pais” antud signaalipinge. Kui see on nt n-pooljuhi korral negatiivne, tõrjutakse voolu kandvaid elektrone eemale, kitsendades voolukanalit ja tõstes selle takistust. Paisuna rakendatakse tihti ka lätte ja paisu vahelise pooljuhipala külgtahusse tehtud pn-siiret. Signaalipinge mõjul hakkab selle siirde tõkkekihi paksus varieeruma, ohjates niiviisi kanali ristlõikepinda ja ühtlasi takistust.

3.3.3 Mis on kiip?

Tänapäeval monteeritakse elektroonikaseadised üksiktransistorite asemel enamasti integraal- ehk terviklülitustest – kiipidest (eesti mugandus ingl. sõnast chip – kild, pala, liistak.) Kiip on pooljuhiplaadike, millesse on tehtud suur hulk imepisikesi, mõnemikromeetriste mõõtmetega transistoreid koos lülitusse kuuluvate takistite, kondensaatorite jm. vajalikuga. Üks kiip moodustab terve võimendi, generaatori või koguni elektronarvuti “peamasina” – protsessori. Viimasel juhul on ainsas mõne cm² suuruses kiibis tuhandeid või koguni sadu tuhandeid transistoreid. Just kiipide kasutuselevõtt on võimaldanud toota ülimalt kompaktset arvutus- ja andmetöötlustehnikat. Kui elektronarvutite algaastail (1950ndail) võtsid need enda alla terveid suuri saale ja vajasid toiteks omaette alajaamu, siis nüüd mahub sama võimas või võimsamgi arvuti lauale, sülle või koguni taskusse.

Kiipe tehakse kavalate aurustus-, söövitus- ja peenkeemiliste protseduuride abil läbi mikroskoopilise mustriga šabloonide ehk maskide.


Kiip.	Nüüdiselektroonika ehituse "suurpaneelid" - kiipidega täidetud trükkplaadid, millele ühendusjuhtmed sadestatakse metalliribadena.

Kokkuvõtteks. Me koondasime tähelepanu tahkiste elektrilistele omadustele. Valik polnud juhuslik. On ju tänapäeva tehnika suuresti elektrotehnika sõna kõige laiemas mõttes – kui mõistame selle all nii elektrienergia tootmist, ülekannet ja tarbimist kui ka elektriliste signaalide saatmist, vastuvõttu, võimendamist ja muundamist ning mitteelektriliste mõjurite ning signaalide teisendamist elektrilisteks (valguse, temperatuuri, rõhu, kalgi kiirguse jne tajurid). Nüüdisinimese tegevuses läheb vaja nii häid elektrijuhte – metalle, pooljuhte kui ka isolaatoreid. Metalle – elektrienergia ülekandeks. Seda pingete-voolude ülilaias vahemikus hiid-kõrgepingeliinidest mikroskoopiliste juhtmeteni kiibis. Dielektrikuid on tarvis voolude “kanaliseerimiseks”, s.o. eri juhtmete, “voolusängide” eraldamiseks. Ja lõpuks kõige paindlikumalt ohjatava juhtivusega materjale – pooljuhte – voolude teisendamiseks, tüürimiseks, tajurite valmistamiseks.

Küsimused ja ülesanded

Toon näiteid nii tehnika arengu headest kui halbadest tagajärgedest.

Kas p-n-siiret sisaldava vooluringi kohta kehtib Ohmi seadus?

Dioodi tingmärgil tähistab nool suunda, milles voolul on “kergem” voolata. Kummal pool noole suhtes on siis n-tüüpi pool?

Stopp! Jäta meelde!

Diood vahelduvvooluringis

Siirdekiht p- ja n-pooljuhi vahel, pn-siire juhib elektrivoolu ainult suunas p-poolmelt n-poolmele; seetõttu toimib vahelduvvooluringi lülitatud p-n-siire (diood) alaldina.

Transistor

Transistor on pooljuhtseadis elektrisignaalide võimendamiseks, muundamiseks ja genereerimiseks.

Kiip ehk terviklülitus

Nüüdiselektroonika põhielement on kiip ehk terviklülitus, milles mõne cm² suurusele pooljuhtplaadikesele on koondatud suur hulk (~ 10...10⁶) üliväikesi transistoreid ühes lisadetailidega, mis toimivad koos tervikliku võimendi, protsessori vm. seadmena.

Testi ennast!

4 Laser. Fotoonika

4.1 Kuidas laser kiirgab

Siin saame teada:

Lisaks iseenesliku elektroni ühelt energiatasemelt teisele liikumisele on olemas ka olukordi, kus sellised üleminekud on sunnitud ehk esile kutsutud. Tulemusena tekib stimuleeritud kiirgus.
On võimalik tekitada olukord, kus aine kiirgab valdavalt stimuleeritud kiirgust. Selline nn pöördhõive on laserit töö aluseks.
Millised on laseri põhiosad, kuidas laser töötab.

4.1.1 Kiirgav aatom

Veepinnal vitsakest vibutades tekitame vee pinnalaineid. Makrofüüsikast teame, et samalaadselt levitavad võnkuvad elektrilaengud elektromagnetlaineid (seda teeb nt kõrgsagedusvool raadiosaatja antennis). Aatomi mikroilma käsitledes oleme seevastu tõdenud, et valguse mikrovälgatusi lähetatakse aatomist kvantsiiretel, üleminekutel energiatasemete vahel. Seejuures ei vihjatud mingitele võnkumistele. Ometi on valguski elektromagnetlainetus. Kas siis elektromagnetlainete kiirgumine makro- ja mikrotasandil on täiesti erinevad protsessid, millel pole midagi ühist? Või on siiski?

Võnkumine on olemuselt perioodiline kohavahetus. Elektroni “koht” aatomis on tema leiulaine. Mikrofüüsikas, kvantfüüsikas seda täpsemalt piiritleda ei saagi. Järelikult tuleb kvantsiiret käsitada kui elektroni võnkumist ühest seisulainest teise, ühest elektronpilvest teise (joon.12.1).

Joon. 12.1. Elektromagnetlaine (footon) kiiratakse, kui elektron võngub ühest leiulainest teise (vrd. joon. 7.2).

Võib ka kujutleda, et kvantsiirde jooksul asub elektron korraga kahes seisulaines. Ainult tõenäosused teda leida ühest või teisest lainest muutuvad siirde käigus: alul on maksimaalne tõenäosus teda tabada ühes, siirde lõpuks aga teises seisulaines. Kvantsiire on protsess, mis toimub lõpliku ajavahemiku jooksul, mitte lõpmata nobe hüpe.

Joon. 12.2. Spektrijooned on erineva intensiivsusega: elavhõbelamp ja intensiivsusjaotus tema spektris.

Seda näeme ka täpsuspiirangust ΔEΔt > h: kui kiirgumisaeg Δt läheneks nullile, peaks ΔE → ∞, ja spektrijoon oleks energiaskaalas lõpmata lai. Tegelikud spektrijooned on üsna kitsad kriipsud (vt. nt. joon. 3.3 ja 3.5), kuigi ka neil, nagu täpsemad uuringud näitavad, on oma lõplik laius, mis võib eri joontel tunduvalt erineda. On ju nii, et kui jooned oleks lõpmata kitsad (ΔE → 0), peaks aatomite kiirgusaktid kestma lõpmata kaua (Δt → 0).

Teisipidi, samast täpsuspiirangust saab joonte laiuse järgi hinnata ka kiirgussiirde kestvust Δt. Osutub, et see on suurusjärgus 10^-9 – 10^-8 sekundit. Üpris lühike aeg muidugi, aga mitte mikromaailma mõõtkavas. Kui arvestada, et valguse võnkesagedus on umb. 10¹⁴ Hz, leiame, et selle ajaga jõuab toimuda sadu tuhandeid kuni miljoneid valgusvõnkeid kiiratavas valguslaines. Käsitades kiiratavat footonit lainejadana, tõdeme, et temasse “mahub” 10⁵ – 10⁶ üksikvõnget temale vastavas laines sagedusega f = c/λ, mis määrab footoni kui osakese energia hf. Kiirgamisaega Δt võib tõlgendada ka kui aatomi ergastatud seisundi iga, kestvust. Et kiirgumine on protsess, toimus, siis võib ea mõiste rakendamine siin tunduda võõristav. Ehk aitaks võrdlus kulleriga, kes saalib kahe linna vahet. Siis võiks seisundi iga vastandada kulleri ametisoleku ajale.

Valguse (footoni) neeldumist võib vaadelda samalaadselt, ainult siis lähtub protsess madalamale energiatasemele vastavast seisulainest (orbitaalist) ja lõpeb suurema energiaga orbitaalil. Ka footoni neeldumisakt toimub lõpliku aja jooksul, mitte momentaanselt.

Nii oleme ka kiirgusprotsessides leidnud silla makro ja mikro vahel.

Kui silmitseda joonspektrite pilte raamatuis, võib näida, et kõik jooned on enamvähem ühesuguse heledusega. See mulje on väär. Vaadeldes spektrijooni lihtsaimaski spektroskoobis, näeme, et mõned jooned on silmatorkavalt heledad, teised nõrgemad, kolmandad vaevumärgatavad. Tähendab, mõne energiaga footoneid kiiratakse tihti, teisi harva; mõnede siirete tõenäosus (toimumissagedus) on suur, teistel väike. Täpsuspiirangu varal hinnates tuleb välja, et eredaid jooni annavad siirded, mis lähtuvad lühiealistest (10^-9 – 10^-8 s) seisunditest, kahvatuid – pikaealistest, nt 10^-3 s. Pikaealisi tasemeid nimetatakse metastabiilseteks (poolstabiilseteks – päris stabiilne on üksnes põhiseisund). Laserites on aatomite metastabiilsed tasemed nendeks vahejaamadeks, kuhu, piltlikult öeldes, kogutakse elektronid ootama märguannet hüppeks, mis vallandab kiirguslaviini.

Siirdetõenäosuste suur erinevus tuleneb looduses üldkehtivatest jäävusseadustest. Kiirgussiiretel peab lisaks energia jäävuse seadusele hf = E_k – E_m, olema täidetud impulssmomendi (pöördeimpulsi) jäävuse seadus. Viimane nõuab, et

(aatomi impulssmoment algseisundis) = (aatomi impulssmoment lõppseisundis) + (footoni impulssmoment).

Kvantarvude keeles: toimuvad üksnes siirded, mille käigus kvantarvu l muutus Δl = ± 1. Kui see nõue pole täidetud, on elektronsiire “keelatud” ehk “ei vasta valikureeglitele”. Seepärast ei leiagi me spektritest mõnede energiatasemete vahedega klappivaid jooni. Nõrgad jooned ilmuvad siis kui aatomis on toimimas vastastikmõjusid, mis leevendavad valikureeglite rangust. Valikureegli Δl = ± 1 kõrval on teisigi, keerukamaid.

4.1.2 Neeldumine, spontaanne ja stimuleeritud kiirgus

Mis juhtub, kui footon tabab ergastatud aatomit?

Vaatame kaht energiataset E_m ja E_k mingis aatomis (joon.13.1). Tabagu aatomit footon energiaga hf_km = E_k – E_m. Kui aatomis on sel hetkel elektron madalamal tasemel E_m, siis footon neeldub, viies elektroni tasemele E_k . (Edaspidi räägime lühiduse huvides lihtsalt aatomist sel või teisel tasemel, mõeldes muidugi elektroni seisundit aatomis.) Elektroni naastes tasemele E_m, kiirgab aatom ise footoni hf_km. See on iseeneslikult tekkiv vaba- ehk spontaanne kiirgus.

Joonis 13.1. Kolm võimalikku siirdeliiki energiatasemete vahel.

Kuid on ju veel võimalus, et footon tabab aatomit parajasti siis, kui too on kõrgemal tasemel E_k. Mis juhtub siis? Neelduda ta ei saa, sest alumisel tasemel ei ole elektroni, millele loovutada oma energia. Ometigi ei jäta footon ka ergastatud aatomit mõjutamata. Kui ta neeldumisel sundis e. stimuleeris elektroni “üles hüppama”, siis nüüd stimuleerib, justkui tõukab ta teda “alla hüppama”, õieti võnkuma seisundite k ja m vahel. Seejuures kiiratakse teine footon sama energiaga hf_km. Sellist kiirgusteket nimetataksegi stimuleeritud kiirguseks ehk sundkiirguseks (vahel ka indutseeritud kiirguseks). Kuid kaotsi ei lähe ka stimuleeriv footon. Aatomist edasi kulgeb nüüd juba kaks footonit. Kujutleme, et aines on hulk aatomeid ergastusseisundis, tasemel E_k. Kui neile langeb footonite hf_km voog (kiirgusvoog), siis iga stimuleeritud kiirgussiire annab voogu ühe footoni juurde. Seega kiirgusvoog mitte ei nõrgenenud, nagu neeldumisprotsessis, vaid võimenes, tugevnes.

Tähelepanuväärne on, et mõlemad footonid on “kaksikvennad”, üksteise eristamatud koopiad. Neil on ühine sagedus f_km ja võnkumised toimuvad neis täpselt ühes taktis (samas võnkefaasis), pealegi samas tasandis. Nad on koherentsed, kooskõlastatud, nende võnkumised ühtuvad nagu hambuvate hammasrataste hambad.

Eeldame, et “üleshüppe” (E_m → E_k) ja “allahüppe” (E_k→ E_m) lähtetasemeil E_m ja E_k on vastavalt N_m ja N_k aatomit. Võib arvata, et “üles” ja “alla” siirete sagedused (siirete arvud ajaühikus) σ_↑ - ja σ_↓ - on võrdelised N_m ja N_k -ga ning mõistagi ka sekundis pealelangevate footonite arvuga ρ:

σ_{↑} = B_{m k} \cdot ρ \cdot N_{m}

σ_{↓} = B_{k m} \cdot ρ \cdot N_{k}

Katsetes on see kinnitust leidnud. Lisaks on kindlaks tehtud, et võrdetegurid B_mk ja B_km on täpselt võrdsed:

B_{m k} = B_{k m} = B

Selle võrdsuse tõttu sõltuvadki footoni šansid, kas neeldudes hukkuda või koos ergastatud aatomiga tütarfootonit sünnitades “ellu jääda”, ainult sellest, kumbi võimalusi on rohkem, kas kohata aatomit seisundis E_m või E_k.

Terane õppur võib nüüd küsida: kas siis kiirguse stimuleerimisel avaldatakse mõju ilma energiat kulutamata – kui stimuleeriv footon kandub edasi täpselt samasugusena kui enne ergastatud aatomiga kohtumist? Vastus on jällegi mikromaailma paradoksides – täpsuspiirangus ΔEΔt∼h. Sundsiire toimub väga lühikese ajavahemiku Δt jooksul. Energia määramatus ΔE on siis väga suur, piltlikult öeldes, sellesse mahub ära ka “allatõukeks” vajalik mõjutamisenergia.

4.1.3 Tavahõive ja pöördhõive

Iga valgusallika valgusse annab oma panuse nii spontaanne kui stimuleeritud kiirgus. Kumb on ülekaalus?

Olgu jällegi meil mingis aatomite kogumis (tahkises, gaasinõus vm) N_m aatomit madalamal tasemel E_m ja N_k aatomit kõrgemal tasemel E_k. Tavaolukorras moodustavad alati lõviosa “energiavaesemad”, footoneid neelavad aatomid: N_m >> N_k. See on energiatasemete tavaasustus e. tavahõive (joon. 13.2). Siis ka siirdesagedused B ⋅ ρ ⋅ N_m>> B ⋅ ρ⋅ N_mja sellises aatomkonnas on ilmselt ülekaalus footonite neeldumine. Vähesed toimuvad kiirgussiirded on valdavalt spontaansed.

Kui mingil viisil õnnestub kunstlikult saavutada kiirgusvõimeliste, ergastatud aatomite ülekaal, “ülakorruse üleasustatus”, pöördhõive, siis kaldub vaekauss stimuleeritud kiirguse poolele (siirdesagedused B ⋅ ρ ⋅ N_k >> B ⋅ ρ ⋅ N_m). Pöördhõive saavutamine on laseriehituse põhiprobleem.

Laser ongi inglise lühendsõna, akronüüm (nagu USA või NATO) väljendist Light Amplification by Stimulated Emission of Radiation - “valguse võimendumine stimuleeritud kiirguse kaudu”.

4.1.4 Pöördhõive tekitamine

Pöördhõiveni jõuda pole põrmugi kerge ega lihtne. Seepärast leiutatigi laserid alles 60ndail aastail, kuigi Albert Einstein oli stimuleeritud kiirguse olemasolu teoreetiliselt tõestanud juba 1916. a.

Kui näiteks üritame pöörata tasemete $E_{m}$ ja $E_{k}$ hõivet, kiiritades aatomeid võimsa valgusvooga sagedusel $f_{m k}$ , jõuame piirjuhul vaid tasakaaluseisundini $N_{m} = N_{k}$ , küündimata pöördhõiveni. (Miks? Vihje: sundsiiretel $E_{m} \to E_{k}$ suureneb $N_{k}$ ja väheneb $N_{m}$ , siiretel $E_{k} \to E_{m}$ on vastupidine toime.) Kui aga otse minna ei saa,ehk siis saab ringi.

Joon. 14.1. Kuidas töötab rubiinlaser? (1) $C r^{3 +}$ – ioonide ergastamine ("ülespumpamine") ksenoonlambi välgatusega. (2) Väledad kiirgusega siirded $E_{a} \to E_{k}$ . (3) Ioonid on kuhjunud metastabiilsele tasemele $E_{k}$ , tekitades pöördhõive $N_{k} > N_{m}$ . (4) Üksikud spontaanselt kiiratud footonid $h f = E_{k} - E_{m}$ vallandavad stimuleeritud kiirguse footonlaviini – lasergiirguse ( $λ = 694, 3 n m$ ).

Et mõne tasemetepaari $E_{k} - E_{m}$ vahel tekiks pöördhõive $N_{k} > N_{m}$ , tuleb appi võtta abitase(med), mille kaudu saaks kuhjata aatomeid ülemisele tasemele $E_{k}$ .

Õnneks on aatomeid, milles eri tasemete vahel toimuvate siirete tõenäosus (ehk ajaühikus toimuvate siirete keskmine hulk) on järsult erinev. Näiteks rubiinikristallis hajusalt paiknevate ioniseeritud kroomiaatomite $C r^{3 +}$ energiatasemete hulgast saab valida kolm taset $E_{m}$ , $E_{k}$ ja $E_{a}$ (abitase!) nii, et siire $E_{a} \to E_{k}$ toimub alatihti, siire $E_{k} \to E_{m}$ seevastu hoopis harvemini, s.o. spontaanse siirde tõenäosus $A_{a k} ≫ A_{k m}$ . Ka tagasisiirded $E_{a} \to E_{m}$ on haruldased. (Siire $E_{a} \to E_{k}$ toimub muide kiirguseta, vabanev energia õhutab kristalliaatomite võnkumisi, so soojendab kristalli.) Seega on seisund $E_{k}$ pikaealine, metastabiilne, keskmise püsivusajaga $τ_{k} \sim 10^{- 3} s$ , seisundi $E_{a}$ umb $100000$ korda lühema ea, $τ_{a} \sim 10^{- 8} s$ vastu.

Valgustame kristalli võimsa välklambiga, mis annab rohkesti rohekassinist, lainepikkuselt üleminekuga $E_{m} \to E_{a}$ ühilduvat valgust. (Ergastuslamp sarnaneb fotovälgutiga, on ainult võrratult eredam.) See paiskab elektrone hulgiti abitasemele Ea, kust nad nobedalt kvanthüppeid $E_{a} \to E_{k}$ sooritades kuhjuvad tasemele $E_{k}$ . Nõnda luuaksegi pöördhõive $N_{k} ≫ N_{m}$ . Nüüd piisab vaid üksikuist spontaansiirdeist $E_{k} \to E_{m}$ , et käivitada footonite “hulgitoodangu” mehhanism – stimuleeritud kiirgusteke.

Joon. 14.3. Protsessid heelium-neoonlaseris. (1) Lahendustoru elektroodide vahel kiirendatud elektronid, põrkudes He-aatomitega, ergastavad viimaseid metastabiilsele taseleme $E_{a}$ . (2) Ergastatud $H e$ -aatomid loovutavad põrgetel oma ergastusenergia $N e$ -aatomeile ( $E - E_{0} = E_{k} - E_{0}$ ); Ne-aatomid kuhjuvad tasemele $E_{k}$ . (3) Üksikud spontaanselt kiiratud footonid $h f = E_{k} - E_{m}$ , tabades metastabiilsele tasemele $E_{k}$ korjunud $N e$ -aatomeid, vallandavad stimuleeritud kiirguse footonlaviini; tase $E_{m}$ tühjeneb kiiresti (kiirguseta) põhitasemele $E_{0}$ .

Gaaslasereis minnakse pöördhõiveni veel kavalamat kaudteed mööda kui rubiinis. Toome näiteks neist ühe kasutatavaima, heelium-neoonlaseri (joon. 14.3). Selles on $H e$ ja $N e$ segu (vahekorras umb $10$ : $1$ ) gaaslahendustorus peeglipaari vahel. Toru sarnaneb neoonreklaamis tarvitatavatega. Ka laseris annavad valgust just Ne aatomid. Gaasi läbiva alalisvoolu toimel ergastatakse nii $H e$ kui ka $N e$ aatomeid. Kuid lisaks ammutab neoon veel hulga ergastusenergiat heeliumilt. Nimelt on $H e$ ergastustase $E_{a}$ $N e$ tasemega $E_{k}$ , ja aatomite põrgetel kandub energia üha heeliumilt neoonile. Et aga $H e$ aatomid on enamuses, on see lisaturgutus üpris tõhus ja pöördhõive $N_{k} > N_{m}$ säilib pidevalt. Pealegi tühjeneb laserisiirde lõpptase $E_{m}$ nobedasti põhitasemele $E_{0}$ , soosides omakorda pöördhõivet. Sisselülitatud $H e$ - $N e$ -laser kiirgab vahetpidamata, ta on alalislaser.

4.1.5 Laseri ehitusest

Joon. 14.2. Nõnda vallandub stimuleeritud valguse fotolaviin.

Joon. 14.4. Nii tekib ja paisub peeglipaari vahel koherentsete footonite laviin laseri kiirguraines (a...e - protsessi järjestikused etapid). Mustad täpid kujutavad ergastamata, punased ergastatud aatomeid, mustad nooled - ergastusvalgust, punased - aatomite kiirgust.

Laseri sünteetiline rubiinikristall töödeldakse silindriks, mille telje pikkus tublisti ületab läbimõõtu. On veel oluline, et ta asetatakse teljega risti rihitud tasaparalleelsete peeglite vahele, optilisse resonaatorisse. (Peeglitena võivad toimida isegi kristalli enda peegelsiledaks poleeritud ja peegeldava kelmega kaetud otsatahud.) Kiirgurkristalli telje suhtes kaldu levivad footonid väljuvad peagi kristallist, kuid telje suunas kiirgunud footonid stimuleerivad üha uusi ja uusi ergastusseisundis kroomiioone (joon. 14.2). Esimesel stimuleeritud kiirguse tekkeaktil saab ühest footonist 2, järgmisel 2st 4, edasi 4→8, 8→16 jne (tegelikult mõnevõrra vähem, kõik footonid ei pruugi märki tabada).

Kiiresti paisub ühesuguste, koherentsete footonite laviin. Piki kristalli leviv valguslaviin peegeldub kummagi peeglini jõudes kristallisse tagasi. Pendeldades kristallis edasi-tagasi, ta aiva võimeneb stimuleeritud kiirguse kaudu (joon. 14.4). Iga peegeldus justkui lisaks uue võimendikristalli. Et kiirt laserist väljastada, tehakse üks peegleist selline, et ta ei peegelda tagasi kogu temale langevat valgust, vaid laseb osa sellest läbi, laserist välja (poolläbitav peegel). Ongi kõik. Kirjeldada kerge, teha raske...

Laseri leiutamise lugu

Laserite leiutamisloos on küllaga põnevust ja dramatismi. Laseri leiutamislugu on suurepärane näide alusuuringute praktilistest viljadest. Mitte keegi ei planeerinud ja kavandanud "projekti" nimega "Ülivalgusallikas laser".

Joon. 14.5. Laser kiirgab sama lainepikkusega valguslaineid samas faasis (koherentselt), Na-lamp – sama lainepikkusega laineid erinevais faasides, hõõglambi valgus on erineva lainepikkusega ning erineva faasiga lainete segu (Optika, lk.37).

Et eristada lasereid kõigist tavavalgusteist, nimetatakse neid mõnikord ka valgusgeneraatoreiks ehk valguse kvantgeneraatoreiks. Sellega rõhutatakse nende sarnasust ja ühtekuuluvust pigem raadiosageduslike lainete generaatoritega raadiojaamades, mis saadavad välja kooskõlastatud, koherentseid elektromagnetlaineid.

Mistahes tavavalgusti (elektripirni, luminestsentslambi, naatriumlambi jne) valgus koostub müriaadidest üksikaatomite mikrosähvatustest. Rõhuvas ülekaalus on üksikaatomite spontaanne, vabakiirgus. Aatomid kiirgavad juhuslikel hetkil, kooskõlastamatult, koherentsitult, arvukail sagedustel ja kõikvõimalikes suundades. Seetõttu on tavavalgusti valgus mittekoherentne, polükromaatne (paljuvärvuslik) liitvalgus, suunatuseta ja suhteliselt nõrk, väikese võimsusega.

Laseris sunnitakse aatomeid sähvatama kooskõlastatult, koherentselt, ühtse “koorina”. Seeläbi on laseri kiirgusvihus valgus koherentne, monokromaatne (ühevärvuslik ja ainusageduslik), suunatud kitsasse vihku ja võib küündida ülivõimsusteni.

Koherentsust hinnatakse koherentsipikkusega l_c, s.o. kiire teekonnaga, mil valgusvõnkumised ei lähe märgatavalt “ühistaktist välja”. Gaaslahenduslampide puhul on l_c mõnikümmend sentimeetrit, laseril võib ulatuda kümnete kilomeetriteni.

Stimuleeritud kiirgusel paljundatakse eeskätt footoneid spektrijoone heledaimast keskosast. Sellest tavatu monokromaatsus. Monokromaatsust tõhustavad omakorda peeglipaari vahel kujunevad valguse seisulained. Need teevad range valiku võimendatavate lainepikkuste hulgas. Täiesti monokromaatset, ühesageduslikku valgust on küll võimatu tekitada, kuid laser ligineb ideaalile. Kui gaaslahenduslambi tüüpilises spektrijoones hälbib valguse lainepikkus joone keskmest umb ± 0,01 nm, siis nt. He-Ne-laseri kiirguses saab hälvet ideaalsest monokromaatsusest kahandada ±10^-6 nanomeetrini.

Stimuleeritud kiirgusaktid pöördhõivestatud keskkonnas toimuvad palju sagedamini kui spontaansed tavakiirguris. Sellest siis rekordiline intensiivsus. Valgusvõimsus jõulise prozhektori valgusvihus võib küündida kilovatini, süsihappegaasil töötava alalislaseri infravalguskiires seevastu 10 kilovatini.

Neodüümklaasist kiirguriga laseri pikosekundilistes välgetes aga ulatub valgusvõimsus mega-, üksikuil hiidlasereil isegi teravattideni. (Võrdle seda hetkvõimsust suurte elektrijaamade alalisvõimsusega!). Kui suvisest otsesest päikesekiirgusest spektraalaparaadiga välja eraldada laseri kiirgusjoonega võrdlaiune riba laseri lainepikkusel, jääb see heleduselt tuhandeid kordi maha isegi tagasihoidliku (~ 1 mW valgusvõimsusega) He-Ne-laseri kiire intensiivsusest, mis on umb. 100 W/m² päikesevalguse ~ 0,025 W/m² vastu.

Lisaks saab koherentset-monokromaatset laserivalgust läätsede abil koondada palju pisemaks täpiks kui tavavalgust. Seeläbi suureneb veelgi pinnaühikule langev valgusvõimsus. On võimalik panna lasereid “tulistama” ülilühikesi valgusimpulsse-välkeid (piko-, isegi femtosekundilise kestvusega, so 10^-12 – 10^-15 s). Nende varal saab uurida ülikiireid mikronähtusi aatomeis, molekulides ja tahkistes. Seega on laserivalgus tavatult kontsentreeritav nii ruumis kui ajas.

Rekordiline on ka laseri valgusvihu suunatus, st. kiirte paralleelsus kimbus. Hälvet paralleelsusest näitab kiirte hajuvus- ehk lahknevusnurk. Väikseim on see gaaslasereil, jäädes mõne nurgaminuti piiresse; lisaoptika aitab seda veel edasi vähendada. See võimaldab laserikiirt kasutada ideaalse kontrollsirgena nt. ehitus- või loodimistöödel, startivate-maanduvate lennukite suunamiseks jpm.

Laserkiirguse hoiatusmärgid (ülemisel: Ettevaatust Laserkiirgus", alumisel: "Ettevaatust! Nähtav ja/või nähtamatu laserkiirgus. Väldi otsese või hajukiirguse sattumist silma või nahale".)

ETTEVAATUST! LASERIKIIR ON OHTLIK!

Isegi suhteliselt nõrk laserikiir, näiteks heelium-neoonlaserist, võib põhjustada silmakahjustusi: silmalääts teravustab selle silma sisemusse ohtlikult eredaks täpiks. Suurema võimsusega laserist silma sattunud kiir võib aga õnnetusohvri jäädavalt pimestada. Seepärast tulebki laseritega töötades tingimata ette panna kasutatavale laseritüübile kohaldatud kaitseprillid. Kunagi ei tohi vaadata otse laserikiirde vastu selle levimissuunda. Kuigi laserit kasutatakse laialt silmaravis, oskavad seda teha vaid vastava väljaõppega meedikud.

Veelgi ohtlikumad on suure võimsusega laserid, nt. tööstuses laialt levinud süsihappegaaslaserid, eriti seetõttu, et nende infravalguskiir on nähtamatu. Nad võivad kahjustada mitte üksnes silmi, vaid kogu keha, suutes hetkeliselt läbi kõrvetada rõivadki, ning tekitada ränki põletushaavu.

Laseriga, isegi näiliselt süütu laserosutajaga loenguruumis ei tohi naljatada, see võib kurvalt lõppeda. Laseraparatuuril, samuti kõigi nende ruumide ustel, kus töötavad laserid, peavad kindlasti olema hoiatusmärgid.

Stopp! Jäta meelde!

Ergastatud kvantseisundi eluiga

Kvantsiirde jooksul võngub elektron aatomis erinevate leiulainete (kvantseisundite) vahel. Ergastatud kvantseisund püsib ~ 10^-9 ... 10^-8 s, pikaealine ehk metastabiilne seisund ~ 10^-3 s.

Stimuleeritud kiirguse tekkimine

Kui footon energiaga hf = E_k - E_m tabab aatomit ergastustasemel E_k, sunnib e. stimuleerib ta aatomit kiirgama. Stimuleeriv ja kiiratud footon on omavahel koherentsed, teineteise täpsed koopiad.

Kiirguslikud siirded

Aatomi vm kvantsüsteemi energiatasemete vahel on võimalikud kolme liiki kiirguslikud siirded: footoni neeldumine, vaba- e. spontaanne kiirgus ja stimuleeritud kiirgus. Footoni šansid ergastamata aatomis neelduda ja ergastatud aatomit kiirgama sundida on võrdsed: B_mk = B_km = B.

Pöördhõive

Aatomite kogumi tavaolekus on ergastamata aatomeid palju rohkem kui ergastatuid (tavahõive, N_k << N_m). Pöördhõive seisundis on mõne tasemepaari hõivatus vastupidine: kõrgem tase on asustatum (N_k > N_m).

Kiirgus pöördhõivestatud aatomite kogumist

Pöördhõivestatud aatomite kogumis ületab stimuleeritud kiirgusaktide sagedus neeldumisaktide oma: BN_k > BN_m.

Laserikiirguse tekkimine

Laserikiirgus tekib stimuleeritud kiirgusaktidel. Laserikiirgurites saavutatakse pöördhõive, kuhjates tugeva ergastusallika toimel aatomeid/molekule metastabiilsetele tasemetele abitasemete kaudu.

Laseri põhiosad

Laseri põhiosad on kiirgur (aktiivaine), ergasti ja optiline resonaator (peeglipaar).

Laserikiirguse omadused

Laserikiirgus on koherentne, monokromaatne, suunatud ja võib olla üliintensiivne; laserikiirgust saab tugevasti kontsentreerida nii ajas (femtosekundilised välked) kui ruumis (mikromeetrised fookustäpid).

Küsimused ja ülesanded

Kuhu “kaob” aatomite ergastusenergia kiirguseta siiretel? Miks on kõigil võimsamail lasereil tõhusad jahutusseadmed?

answer

Ühe laseritüübi valgusvihu lahknevusnurk on

0, 05^{\circ}

. Arvuta, kui kaugel silmast peaks olema tuletikk, et tema jämedus (ca

2 m m

) paistaks sama nurga all.

answer

4.2 Laserid ja fotoonika

4.2.1 Laserid teadustöös

Tänapäeval on raske leida füüsika haru, mille arendamises sel või teisel kombel ei osaleks laserid või vähemasti nendega seotud ideed. Näiteks on nüüdisspektroskoopia valdavalt laserspektroskoopia. Selles on märkimisväärseid teeneid ka Eesti teadlastel. Tartust Füüsika Instituudist on alguse saanud üks laserspektroskoopia eriti suure täpsusega meetod: spektrite lasersälkamine.

Laserite tulekuga astus vana klassikaline, justkui ammu lõplikult valmis teadusharu optika uude ajastusse, sündis mittelineaarne optika. Selgub, et ülieredas laserivalguses muutub paljude optikanähtuste iseloom ja ammutuntud optikaseadused kaotavad seal jõu. Nii näiteks ei pruugi mittelineaarses optikas peegeldumisnurk võrduda langemisnurgaga. Saab genereerida “valguse ülemtoone”, st osa laserikimbust sagedusel $f$ muutub teatavais kristallides valguseks sagedusel $2 f$ , $3 f$ jne. Fotoefektil suudab ainest elektroni välja paisata mitte üksnes footon energiaga $h f = A$ , vaid ka mitu ( $2$ , $3$ jne) footonit “ühisel jõul”, kui vaid nt. $h f_{1} + h f_{2} = A$ , kus $f_{1}$ ja $f_{2}$ on kummagi footoni sagedused ja $A$ väljumistöö. Selleks peab muidugi valgusvoog olema väga tugev, et oleks piisavalt suur tõenäosus kahe footoni kohtumiseks ühe elektroni juures.

Keemias (ka keemiatööstuses) mõjutatakse laseriga kiiritades reaktsioonide käiku, suurendades vahel tuhandeid kordi protsesside kiirust.

Bioloogias tehakse laserikiirega peenoperatsioone rakkudel ja mikroorganismidel, koguni pärivusaine DNA hiidmolekulidel.

Maakaartide valmistamist ja täpsustamist on tõhustanud laserkaugusmõõturid ja -nivelliirid (pinnareljeefi määramise aparaadid).

Loetelu võiks aiva pikendada, kui see ei muutuks tüütuks.

Tänapäeva tehnikasse ja teadusse on astunud elektroonika kõrvale fotoonika – laserite koherentvalguse kasutamine. Elektroonikat välja tõrjumata täiendab ja avardab ta võrratult tehnika võimalusi. Näiteks on põhjust arvata, et 21. sajandi arvutus- ja infotehnika põhineb suuresti fotoonikal.

4.2.2 Laserite pere

Laserite pere on üliarvukas. On välja otsitud sadu aatomite, ioonide ja molekulide liike, mille energiatasemete hulgas leidub pöördhõivestamiseks sobivaid. Seejuures oli hindamatu väärtusega paljude spektroskopistide aastakümnetepikkuse usina töö viljana korjunud teave. Nii näeme, et esmapilgul vägagi akadeemilised ja elukauged uuringud võivad ühel hetkel osutuda praktikale üpris vajalikeks. Tänu sellele mitmekesisusele sai valmistada lasereid, mis genereerivad koherentset valgust erinevatel lainepikkustel, mis langevad laia vahemikku – kaugest ultravalgusest üle nähtava spektririba kauge infravalguseni (umb. 0,2 μm kuni 11 μm, vt tabel raamatu lõpus). On ka lasereid, mille lainepikkust saab kitsamas vahemikus sujuvalt muuta. See on eriline voorus teadusuuringuis, nt spektroskoopias. Loomisel on röntgenikiirguse laserid (raserid). Laserkiirguritena (laseri aktiivainetena) toimivad nii tahkised (kristallid, klaasid), vedelikud (eriti mitm. orgaaniliste värvainete lahused) kui ka gaasid ning metallide aurud (soositud on heeliumi-neooni segu, süsihappegaas, argoon, krüptoon, lämmastik, vaseaurud). Eri aktiivained nõuavad erinevaid ergastusviise pöördhõive tekitamiseks e. “ülespumpamiseks”. Tahkis- ja vedeliklasereid ergastatakse võimsate valgusallikatega - välklampide või ka teiste laseritega. Laserigaasides ja -aurudes tekitatakse “pumpamiseks” elektrilahendus. Suuresti varieeruvad ka laserite mõõtmed. On unikaallasereid, mis täidavad hiigelsaale, hulgiti toodetakse ja tarbitakse siiski pisikesi – nööpnõelapea suurustest pooljuhtlaseritest nii umbes pastakamõõduliste gaaslaseriteni. Omaette rühma moodustavad pooljuhtlaserid.

Pooljuhtlaser ehk dioodlaser on kohaselt valmistatud valgusdiood, millest juhitakse läbi teatavast läviväärtusest tugevam pärivool. Erinevalt tavalisest valgusdioodist annab ta koherentvalgust. Pöördhõive tekitatakse voolu abil kristalli juhtivus- ja valentsitsooni vahel pn-siirde piirkonnas. Sageli tehakse laserdioode ka erinevate pooljuhtühendite kihtidest, kasutades p-n-siirete asemel heterosiirdeid eri ainete vahel (kr. heteros – teine, muu). Laseripeegleina võivad toimida pn-siirdega ristsuunalised kristalli vastastahud (vt. joon. 15.1). Tänu oma väiksusele, tõhususele (kasutegur 20 – 30 % teiste laserite mõne protsendi vastu) ja odavusele on pooljuhtlaser nüüd kõige laiemalt kasutatavam laseriliik. Igal aastal toodetakse ja turustatakse neid miljonite viisi. Nad töötavad laserkassaatoris, laserprinteris, lasergrammofonis, arvuti kompaktkettamälu (CD-ROM) lugejais jpm. Nende kogumeid on hakatud kasutama ergastitena (s.o. pöördhõive tekitamiseks kiirguris) ka rubiinlaseri sarnastes tahkislasereis.

See mitmekesisus võimaldab laseri paindlikku valikut vastavalt kasutusviisile. Mõnikord on vaja rekordilist monokromaatsust, võimsus ei ole aga oluline, teisal jälle vastupidi, on oluline vaid hiiglaslik valgusvõimsus. Järsult erinevad nõuded ongi ajendanud nii paljude erinevate laseritüüpide loomist.

4.2.3 Laserid ametis

Tänapäeval puutume laserseadistega kokku iga päev.

Ühe paeluvaimaga laserite rakendustest – holograafiaga tutvusime juba optikakursuses. Näitustel ja muuseumides võime näha üllatavalt originaalisarnaseid ruumpilte – hologramme. On ateljeesid, kust võib tellida endagi hologrammportree. Viisadel, pangakaartidel jm näeme veiklevaid holograafilisi turvatähiseid, mida on väga raske võltsida. Ajakirjades ja raamatutes rõõmustavad aegajalt silma trükkhologrammid.

Kauplustes loeb laserkassaator kauba ribakoodilt hetkeliselt selle hinna ja nimetuse ning trükib kassatšekile.
Arvutil koostatud tekste ning lisatud jooniseid trükib kvaliteetselt välja laserprinter. Käesoleva õpikugi käsikiri ja makett on tehtud laserprinteri abil.
Heli- ja videosalvestina on üldlevinud laserplaat (ehk kompaktketas, ingl. CD – Compact Disc). Peale tippkvaliteediga heli- ja videosalvestuse kasutatakse kompaktplaate ka arvutites suurte teabehulkade, sh nt värvipiltide salvestamiseks ja lugemiseks-vaatamiseks.
Kui kõneleme telefoniga, saadame faksi või raalpostikirja (ingl. electron mail, e-mail) või vaatame kaabeltelevisiooni, läbib teade või saade vähemalt osa oma teekonnast saatjast vastuvõtjani mööda optilist kaablit, milles infot kannab laserikiir, mis levib mööda peenest läbipaistvast kvartskiust punutud valgusjuhtmeid. Tänu valguse kõrgele võnkesagedusele, mis miljoneid kordi ületab raadiosagedusi, saab koherentsele valguslainele “kirjutada” ülisuuri teabehulki. Ainsat laserkanalit mööda saab edastada korraga kümneid tuhandeid telefonikõnesid või kümneid teleprogramme.
Paljudel suurtel lennuväljadel ja sadamates aitavad lendureid ja tüürimehi lasernavigatsiooniseadmed.

Meditsiinis on laserid rakendust leidnud peaaegu kõigis selle eriharudes, nii haiguste diagnostikas kui ka ravis, eriti kirurgias.

Juba aastakümneid on laserid tarvitusel silmakliinikuis: hõlpsasti silma juhitava laserikiirega saab mitmeid raskeid silmarikkeid parandada ilma seni vältimatu kirurgilise sekkumiseta, seejuures peaaegu vaevusteta, sageli ambulatoorselt, patsienti haiglasse võtmata.

Kirurgias on laserskalpelli oluliseks eeliseks tema täielik steriilsus ja “veretus”: kõrvetades (kauteriseerides) peenemate veresoonte lõikekohti, ta ühtlasi suleb need. Võrratu eelis on ka see, et peeni kiudvalgusjuhtmeid kaudu saab võimsat laserikiirt juhtida tõvestatud kohta mitmesugustes kehaõõntes, soontes jne, ilma neid lõikeriistaga (kirurgiliselt) avamata. Saab nt pihustada neeru-, sapi- ja põiekive, kõrvaldada lubiladestusi veresoontes. Viies ohtlikesse kasvajatesse teatavaid pigmente, lagunevad kasvajad paljudel soodsatel juhtudel laserkiirituse toimel. Kaariesest tabatud hambasäsi kõrvaldab täpselt ja valutult laserhambapuur.

Tehnoloogias on võimsad laserikiired (eriti tänu nende heale teravustatavusele) leidnud laialdast kasutamist erinevate töötlusvõtete sooritamiseks: märkimiseks, puurimiseks, lõikamiseks-tükeldamiseks, korrosioonivastaseks pinnatöötluseks. Võrreldes tavaseadistega on lasertööpingid hõlpsamini automatiseeritavad, raalohjele viidavad. Töödelda saab lausa kõiksuguseid materjale: metalle, plastikuid, keraamikat, puitu, koguni riiet (rõivaste juurdelõikuseks paketiviisil). Metallipulbreid võib paagutada keerulise kujuga detailideks. Näiteks tänapäeva moderniseeritud autotehastes (eriti Jaapanis ja USAs) sooritatakse valdav osa (70 – 80%) keevitusoperatsioonidest autokerel robot-laseragregaatidel. Keevis saab eriti puhas ja täpne ega vaja järeltöötlust. Ka Eesti tööstuses pole lasertööpink enam harulduseks.

Stopp! Jäta meelde!

Fotoonika

Nüüdistehnikasse on elektroonika kõrvale astunud fotoonika: laserite koherentsete footonivoogude kasutamine.

Laserite tüübid

Levinuimad laseritüübid on pooljuht-, tahkis- ja gaaslaserid.

Laserite kasutusvaldkonnad

Lasereid kasutatakse olmes (automaatkassaatorid, grammofonid, printerid, holograafiatooted), meditsiinis (kirurgia, diagnostika, ravikiiritus), tööstuses (lõikamine, puurimine, keevitamine), sides (eriti optiliste kiudliinide kaudu), teadusuuringutel jpm.

Küsimused ja ülesanded

Miks on hologrammide valmistamiseks (holografeerimiseks) tarvis laserit?