Kuidas planeedid kosmoselaeva kiirendavad

Tegelikult muidugi ei ole nii, et kosmoses liiguvad kehad ühtlaselt ja sirgjooneliselt. Gravitatsioonijõud küll väheneb võrdeliselt kauguse ruudu pöördväärtusega, aga see ikkagi pidurdab. Kui suure kiiruse peaks andma Maalt lahkuvale kosmoselaevale, et see jõuaks päikessüsteemist välja? Kas teel on võimalik kineetilist energiat juurde saada?

Oletame, et kogu kosmoselaeva kineetiline energia tuleks sellele anda kohe pärast starti. Kui suur see peaks olema? Toome sisse paokiiruse mõiste.

Paokiirus

Keha suudab ületada massiga $M$ ja raadiusega $R$ astronoomilise keha gravitatsioonilise külgetõmbe (s.t suudab lahkuda lõpmata kaugele), kui tema kiirus astronoomilise keha pinna lähedal on vähemalt võrdne paokiirusega, mis on arvutatav valemist

(13-28)

v = \sqrt{\frac{2 G M}{R}}

Täpsemalt võib lugeda siit:

Paokiirus

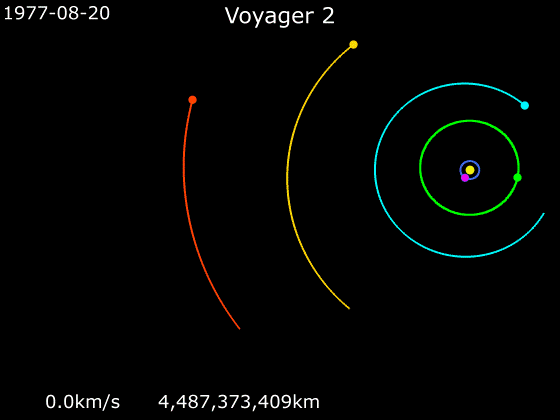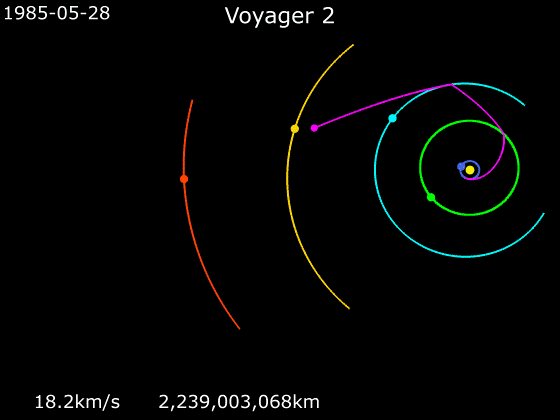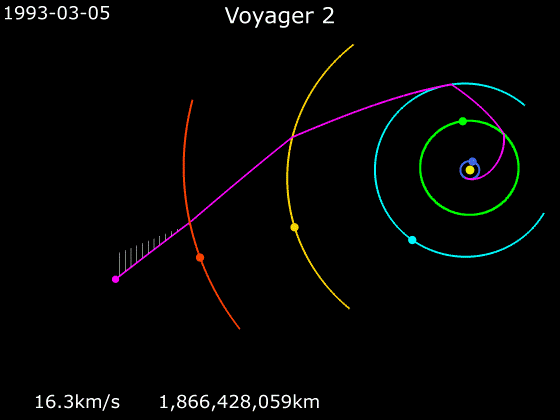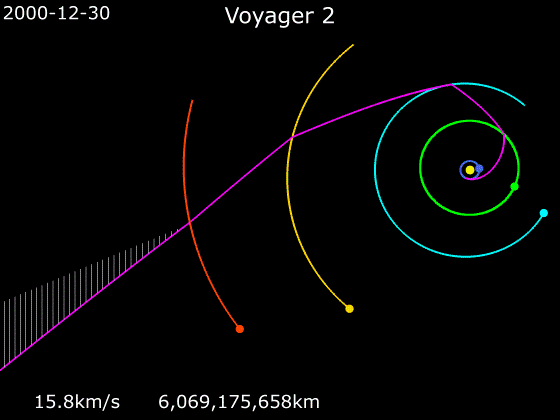
Kui tulistada mürsk vertikaalselt üles, siis enamasti ta liikumine järjest aeglustub, siis mürsk peatub hetkeks ja lõpuks langeb tagasi Maale. Kui aga mürsk saab teatud miinimumväärtusest suurema algkiiruse, siis tema liikumine küll aeglustub, aga teoreetiliselt saab kiirus nulliks alles lõpmata kõrgel.

Voyager 2 kiiruse graafikut uurides (vt allpool) näeme, et ehkki Voyager 2 algkiirus oli vägev, vähenes see Maast eemaldudes väiksemaks kui päikesesüsteemist lahkumise paokiirus. See on ka arusaadav - ületada tuleb ka Maa gravitatsioonijõud. Aga päikesesüsteemi planeetidest möödudes juhtub midagi?

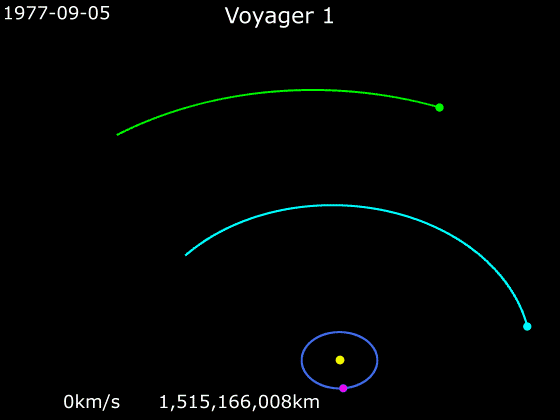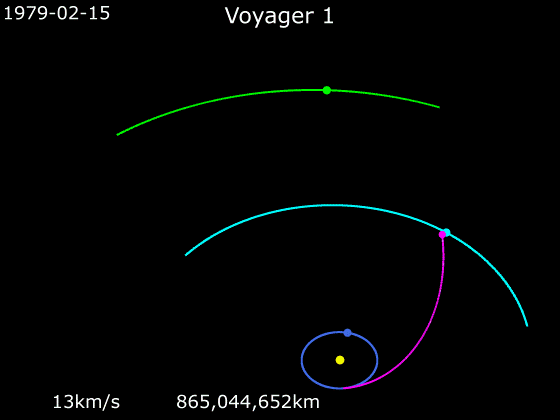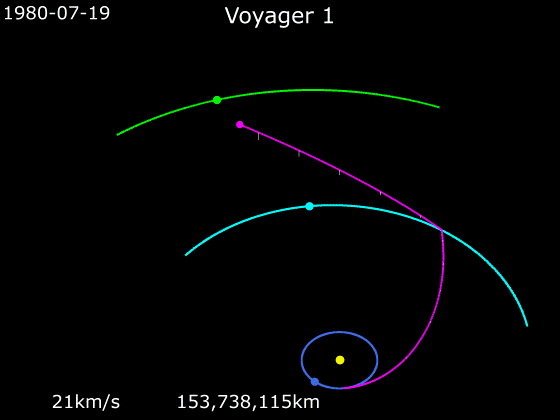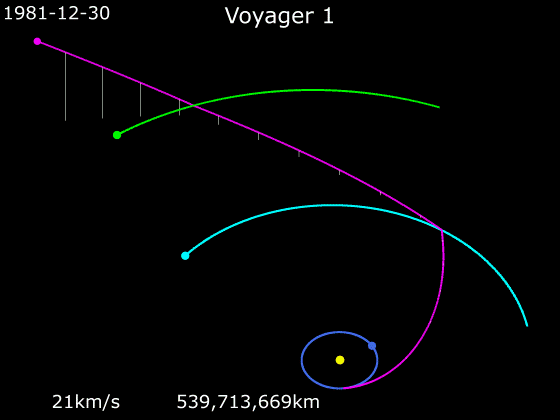
Voyager 2 kiirus päikesesüsteemis ja sellest lahkudes

Kosmoselaevade kiirendamiseks ja aeglustamiseks on tavaline meetod nn gravitatsiooniline lingutamine, kus kosmoselaeva trajektoor ristub kiiresti liikuva planeedi orbiidiga, planeet tõmbab kosmoselaeva gravitatsioonijõu vahendusel endaga kaasa ja kiirendab seda iseenda kineetilise energia arvelt.

Järgnevad kaks animatsiooni näitavad, kuidas nägid välja kosmoselaevade Voyager 1 ja Voyager 2 trajektoorid, kui need liikusid läbi päikesesüsteemi. Jälgige animatsioonide all servas kosmoselaevade kiiruseid.


Animatsioonis möödub Voyager 1 (magenta joon) kõigepealt Jupiterist (tsüaan orbiit), siis Saturnist (roheline orbiit). Alumises vasakus nurgas on näha Voyageri kiirus, mis Jupiterist möödudes suureneb tunduvalt tänud linguefektile (gravity assist), kus Jupiter gravitatsiooniväljaga tõmbab Voyageri endaga kaasa, muutes ühtlasi kosmoselaeva suunda. Kujutatud on teekond 5. septembrist 1977 kuni 30. detsembrini 1981.	Animatsioonis möödub Voyager 2 (magenta joon) Jupiterist (tsüaan orbiit), Saturnist (roheline orbiit), Uraanist (kollane orbiit) ja Neptuunist (punane orbiit). Alumises vasakus nurgas on näha Voyageri kiirus, mis planeetidest möödudes suureneb tänud linguefektile (gravity assist), kus planeetide gravitatsiooniväljaga tõmbab Voyager 2 endaga kaasa, muutes ühtlasi kosmoselaeva suunda. Kujutatud on teekond 20. august1977 kuni 31. detsembrini 2000.

Animatsioonis möödub Voyager 1 (magenta joon) kõigepealt Jupiterist (tsüaan orbiit), siis Saturnist (roheline orbiit). Alumises vasakus nurgas on näha Voyageri kiirus, mis Jupiterist möödudes suureneb tunduvalt tänud linguefektile (gravity assist), kus Jupiter gravitatsiooniväljaga tõmbab Voyageri endaga kaasa, muutes ühtlasi kosmoselaeva suunda. Kujutatud on teekond 5. septembrist 1977 kuni 30. detsembrini 1981.

Animatsioonis möödub Voyager 2 (magenta joon) Jupiterist (tsüaan orbiit), Saturnist (roheline orbiit), Uraanist (kollane orbiit) ja Neptuunist (punane orbiit). Alumises vasakus nurgas on näha Voyageri kiirus, mis planeetidest möödudes suureneb tänud linguefektile (gravity assist), kus planeetide gravitatsiooniväljaga tõmbab Voyager 2 endaga kaasa, muutes ühtlasi kosmoselaeva suunda. Kujutatud on teekond 20. august1977 kuni 31. detsembrini 2000.