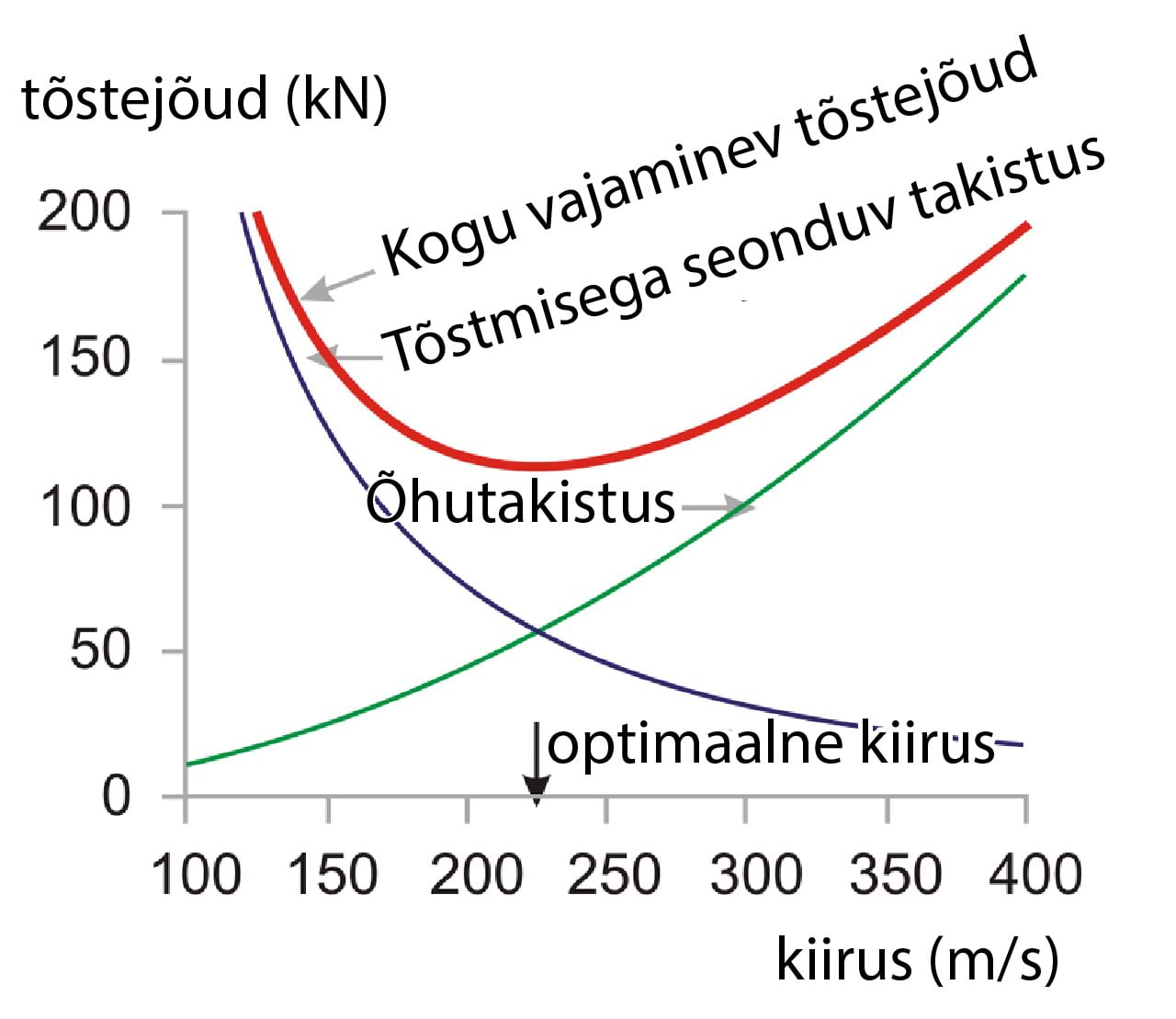
Lennuki liikumas hoidmiseks vaja minev energia sõltuvana kiirusest

Lennuki liikumas hoidmiseks vaja minev energia sõltuvana kiirusest $v_L$ on takistusjõu $\frac{1}{2} c_d \rho_\text{õ} A_pv_L^2$ – mis suureneb kiiruse kasvades – ja tõstmiseks kuluva jõu (tuntud ka kui indutseeritud takistus) $\frac{1}{2} \frac{(mg)^2}{ \rho_\text{õ} v^2A}$ – mis väheneb kiiruse suurenedes – summa. On olemas kirus $v_\text{optimaalne}$, mille korral vajalik jõud on minimaalne. Jõud on energia teepikkuse kohta, nii et minimiseerides jõu minimiseerime me ka teepikkuse kuluva kütuse hulga. Et kütuse kasutust optimiseerida peame me lendama kiirusel $v_\text{optimaalne}$. See joonis näitab kilonjuutonites meie lihtsa mudeli hinnangut, millist jõudu on erinevate kiiruste $v$ korral tarvis $317$ tonni kaaluva, $64$ meetrise tiivaulatusega, $0,03$ takistuskoefitsiendiga ja $180\, \mathrm{m^2}$ esiosa pindalaga Boeing 474 lendamiseks, kui õhu tihedus on $\rho = 0,41\, \mathrm{kg/m^3}$ ($10\, \mathrm{km}$ kõrgusel). Meie mudel pakub optimaalseks kiiruseks $v_\text{optimaalne} = 220\, \mathrm{m/s}$ ($540 \, \mathrm{mph}$). Õhusilindriga tegeleva mudeli jaoks on see võrdluses tegelikkusega väga hea tulemus!