Elektrivoolu magnetväljad (Füüsika põhikursus)

Elektrivoolu magnetväljad

Füüsiku pilguga

Kui loed seda lauset, siis on teatud piirkond Su ajus aktiveeritud. Kui nuusutad roosi või tunned pliiatsit oma käes, siis on aktiveeritud mõned teised piirkonnad. Üks parimatest meetoditest määramaks, millised piirkonnad ajus on aktiivsed, on jälgida aktiivsusega kaasnevat magnetvälja. Sellel fotol kujutatud aparaat suudab registreerida magnetvälju, mis tekivad inimese ajutegevuse käigus, nii et aju aktiivsusjaotust saab siduda inimese tegevusega. Kuid ajus ei ole magnetilisi materjale. Niisiis: kuidas on võimalik, et ajutegevuse aktiivsus tekitab magnetvälja?

Füüsika ühe olulise tähelepaneku kohaselt on liikuvate laetud osakeste ümber magnetväli. Järelikult on ka liikuvate laetud osakeste ehk elektrivooluga juhtme ümber magnetväli. Selline elektromagnetism, mis hõlmab korraga nii elektrilisi kui ka magnetilisi nähtusi, oli oma avastajatele üllatuseks. Kuid olgu üllatus või mitte, on see nähtus muutunud meie igapäevaelus ülimalt tähtsaks, sest see on aluseks lõputule reale elektromagnetilistele seadmetele. Elektrivoolu magnetvälja saab leida aparaatides, mis salvestavad või loevad magnetiliselt kodeeritud magnetlinte ja kettaid nagu praegu juba vanamoodsad arvutidisketid, kassettmagnetofoni helilindid ning videomaki videolindid. Magnetväli mängib olulist rolli ka magnet-hõljukrongides ja paljudes seadmetes, mis on kasutusel raskete koormate tõstmiseks.

Meie esimene samm selles peatükis on leida vooluga juhtme väga lühikese lõigu magnetväli. Edasi arvutame kogu juhtme magnetvälja mitmete erikujuliste juhtmete korral.

Elektrivoolu magnetvälja arvutamine

JOONIS 29-1 Voolu-pikkuse element $i d \to s$ tekitab diferentsiaalse magnetvälja $d \to B$ punktis $P$ . Roheline $\times$ (noole saba) punkti $P$ asukohas näitab, et selles punktis on $d \to B$ suunatud lehekülje tasandi sisse.

Joonisel 29-1 on näidatud suvalise kujuga juhe, mida läbib vool $i$ . Soovime leida magnetvälja $\to B$ punkti $P$ ümbruses. Esmalt jagame mõtteliselt juhtme diferentsiaalseteks elementideks $d s$ ning siis määrame iga elemendi jaoks pikkusvektori $d \to s$ , mille pikkus on $d s$ ja mille suund ühtib voolu suunaga elemendis $d s$ . Edasi määratleme diferentsiaalse voolu-pikkuse elemendi kui korrutise $i d \to s$ ; me tahame leida punktis $P$ magnetvälja $d \to B$ , mida tekitab tüüpiline voolu-pikkuse element. Katsetulemustest on teada, et nagu elektrivälju, võib ka magnetvälju üksteisele liita ja saada nii summaarne magnetväli. Seega saame arvutada summaarse magnetvälja $\to B$ punktis $P$ integreerimise teel üle kõikide diferentsiaalsete magnetväljade $d \to B$ , mis on tekitatud kõikide voolu-pikkuse elementide poolt. Kuid selline summeerimine on vaevarikkam kui analoogne arvutus elektriväljade jaoks, sest laenguelement $d q$ , mis elektrivälja tekitab, on skalaarne suurus, kuid voolu-pikkuse element $i d \to s$ on vektor, sest see on vektori ja skalaari korrutis.

Välja $d \to B$ suurus punktis $P$ , mis asub kaugusel $r$ voolu-pikkuse elemendist $i d \to s$ , avaldub kujul

(29-1)

d B = \frac{μ_{0}}{4 π} \frac{i d s sin θ}{r^{2}}

kus $θ$ on suundade $d \to s$ ja $^r$ , mis on ühikvektor suunaga elemendist $d s$ punkti $P$ , vaheline nurk. Sümbol $μ_{0}$ on konstant, mis kannab nime magnetiline konstant ja mille väärtus on definitsiooni järgi täpselt

(29-2)

μ_{0} = 4 π \times 10^{- 7} T \cdot m / A \approx 1, 26 \times 10^{- 6} T \cdot m / A

Magnetvälja $d \to B$ suund, mis joonisel 29-1 on suunatud lehekülje tasandi sisse, ühtib vektorkorrutise $d \to s \times \to r$ suunaga. Seepärast saame kirjutada valemi 29-1 vektorkujul:

(Biot-Savart'i seadus, 29-3)

d \to B = \frac{μ_{0}}{4 π} \frac{i d \to s \times^r}{r^{2}}

Saadud vektorvalem ja selle skalaarse kuju valem 29-1 on tuntud Biot’-Savart’i seadusena. See seadus, mis on tuletatud katsest, annab magnetvälja suuruse pöördvõrdelisena kauguse ruuduga. Me kasutame seda selleks, et leida mitmesuguste voolujaotuste summaarset magnetvälja $\to B$ voolu ümbritseva ruumi suvalises punktis.

Pika sirge vooluga juhtme magnetväli

Kasutame Biot’-Savart’i seadust tõestamaks, et vooluga $i$ (lõpmata) pika sirge juhtme magnetvälja suurus on

(pikk sirge juhe, 29-4)

B = \frac{μ_{0} i}{2 π R}

Magnetvälja suurus $B$ valemis 29-4 sõltub vaid voolust ja punkti kaugusest $R$ juhtmest, mõõdetuna risti juhtmega. Valemi tuletamisel näitame, et välja $\to B$ jõujooned on kontsentrilised ringjooned juhtme ümber, mida on näha joonisel 29-2 ja millele viitab ka rauapuru joonisel 29-3. Jõujoonte vahekauguse suurenemine joonisel 29-2 kauguse suurenemisel juhtmest on kooskõlas magnetvälja $\to B$ suuruse vähenemisteguriga $1 / R$ valemis 29-4. Kahe väljavektori $\to B$ pikkused joonisel näitavad samuti magnetvälja suuruse vähenemist võrdeliselt teguriga $1 / R$ .


JOONIS 29-2 Pikas sirges juhtmes oleva voolu magnetvälja jõujooned on kontsentrilised ringjooned ümber juhtme. Joonisel on vool suunatud lehekülje sisse, mida näitab ka tähis $\times$ .	JOONIS 29-3 Rauapuru, mis on puistatud papptahvlile, asetub kontsentriliste ringidena, kui vool läbib keskset juhet. Selline rauapuru asetus piki magnetvälja jõujooni on põhjustatud voolu poolt tekitatud magnetväljast. (Foto avaldatud Education Development Centeri loal)

Voolu-pikkuse elemendi magnetvälja suunda saab leida parema käe reegli abil:

parema käe reegel: haara voolu-pikkuse element oma paremass kätte nii, et väljasirutatud pöial näitab voolu suunda. Siis kõverduvad Su sõrmed juhtme ümber vooluelemendi poolt tekitatud magnetvälja jõujoonte suunas.

JOONIS 29-4 Parema käe reegel annab vooluga juhtme magnetvälja suuna. (a) Joonisel 29-2 kujutatud situatsioon külgvaates. Magnetväli $\to B$ suvalises juhtmest vasakul asetsevas punktis on risti radiaalse punktiirjoonega ja suunatud lehekülje tasandi sisse sõrmedega näidatud suunas, mida näitab ka tähis $\times$ . (b) Kui muuta voolu suund vastupidiseks, siis on magnetväli $\to B$ suvalises juhtmest vasakul asetsevas punktis ikka suunatud risti radiaalse punktiirjoonega, kuid nüüd on see suunaga lehekülje tasandist välja, mida näitab ka tähis $\cdot$ .

Parema käe reegli rakendamise tulemus vooluga sirge juhtme korral joonisel 29-2 on näidatud joonisel 29-4a külgvaates. Selleks, et määrata voolu magnetvälja $\to B$ suund suvalises punktis, tuleb mõtteliselt haarata parema käega ümber juhtme nii, et pöial näitaks voolu suunda juhtmes. Kui sõrmeotsad on vaadeldavas punktis, siis on sõrmede suund magnetvälja suund selles punktis. Vastavalt joonisele 29-2 on magnetväli $\to B$ igas punktis magnetvälja jõujoone puutuja suunaline; vastavalt joonisele 29-4 on magnetväli suunatud risti radiaalsele punktiirjoonele, mis ühendab seda punkti ja voolu.

Valemi 29-4 tõestus

Joonis 29-5 on sarnane joonisega 29-1, välja arvatud see, et nüüd on juhe vastavalt käesolevale ülesandele sirge ja lõpmata pikk. Tahame leida magnetvälja $\to B$ punktis $P$ , mis asub juhtmest ristsuunas kaugusel $R$ . Diferentsiaalse magnetvälja suurus, mille tekitab voolu-pikkuse element $i d \to s$ , on elemendist kaugusel $r$ asuvas punktis $P$ antud valemiga 29-1:

d B = \frac{μ_{0}}{4 π} \frac{i d s sin θ}{r^{2}}

JOONIS 29-5 Pika sirge vooluga $i$ juhtme magnetvälja arvutamine. Nagu näha jooniselt, on punktis $P$ voolu-pikkuse elemendi $i d \to s$ tekitatud magnetväli $d \to B$ suunatud lehekülje tasandisse.

Diferentsiaalse magnetvälja $d \to B$ suund joonisel 29-5 ühtib vektori $d \to s \times \to r$ suunaga ja on suunatud lehekülje tasandisse.

Märgime, et $d \to B$ punktis $P$ on ühesuguse suunaga kõikide voolu-pikkuse elementide korral, milleks juhe on jagatud. Seega saame leida lõpmata pika juhtme ülemise poole voolu-pikkuse elementide summaarse magnetvälja suuruse punktis $P$ , integreerides $d B$ avaldist 29-1 rajades $0$ kuni $\infty$ .

Nüüd vaatleme voolu-pikkuse elementi juhtme alumises pooles, mis asub kaugel allpool punkti $P$ , niisamuti nagu $d \to s$ asub ülalpool punkti $P$ . Vastavalt valemile 29-3 on voolu-pikkuse elemendi magnetväli punktis $P$ sama suuruse ja suunaga kui elemendi $i d \to s$ poolt tekitatud magnetväli joonisel 29-5. Seetõttu on vooluga juhtme alumise poole tekitatud magnetväli täpselt samasugune kui juhtme ülemise poole poolt tekitatud magnetväli. Summaarse magnetvälja $\to B$ suuruse leidmiseks punktis $P$ on vaid vaja integreerimise tulemus korrutada teguriga $2$ . Seega saame

(29-5)

B = 2 \int_{0}^{\infty} d B = \frac{μ_{0} i}{2 π} \int_{0}^{\infty} \frac{sin θ d s}{r^{2}}

Muutujad $θ$ , $s$ ja $r$ ei ole selles valemis üksteisest sõltumatud. Joonis 29-5 näitab, et need on omavahel seotud valemitega

r = \sqrt{s^{2} + R^{2}}

sin θ = sin (π - θ) = \frac{R}{\sqrt{s^{2} + R^{2}}}

Asetades need seosed valemisse ja kasutades integraali 19 Lisas E, saame valemi 29-5 kirjutada kujul

(29-6)

B = \frac{μ_{0} i}{2 π} \int_{0}^{\infty} \frac{R}{{(s^{2} + R^{2})}^{3 / 2}} = \frac{μ_{0} i}{2 π R} {[\frac{s}{{(s^{2} + R^{2})}^{1 / 2}}]}_{0}^{\infty} = \frac{μ_{0} i}{2 π R}

mis ongi just see seos, mida tahtsime tõestada. Märgime, et lõpmata pika vooluga juhtme ülemise või alumise poole magnetvälja suurus punktis $P$ joonisel 29-5 võrdub poolega selles valemis antud magnetvälja suurusest, s.t

(poollõpmatu sirge juhe, 29-7)

B = \frac{μ_{0} i}{4 π R}

Poolkaare-kujulise vooluga juhtme magnetväli

Selleks, et leida kõverat juhet läbiva voolu magnetvälja, võiksime taas valemi 29-1 alusel kirjutada ühe voolu-pikkuse elemendi magnetvälja suuruse ja integreerida seda üle kõikide voolu-pikkuse elementide, et leida kogu juhet läbiva voolu summaarne magnetväli. Kuid see integreerimine võib osutuda juhtme kujust sõltuvalt keerukaks. Lihtne on see vaid siis, kui juhtmel on poolkaare kuju ja kui punkt, kus välja suurust määrata soovitakse, asub kaare kõveruskeskmes.

JOONIS 29-6 (a) Ringikaare kujulist juhet, mille kõveruskese asub punktis $C$ , läbib vool $i$ . (b) Juhtme iga elemendi jaoks kaarel on nurk suundade ds ja r vahel võrdne $90^{\circ}$ . (c) Juhtmes oleva voolu tekitatud magnetvälja suuna määramine punktis $C$ ; magnetvälja suund on lehekülje tasandist välja sõrmeotste suunas, nagu on näidatud joonisel värvilise täpiga punktis $C$ .

Joonisel 29-6a on kujutatud selline kaarjas juhe kaare kesknurgaga $ϕ$ , raadiusega $R$ ja kõveruskeskmega $C$ , mida läbib vool $i$ . Juhtme iga voolu-pikkuse element $i d \to s$ tekitab punktis $C$ magnetvälja suurusega $d B$ , mis on määratud valemiga 29-1. Nagu näitab joonis 29-6b, on nurk $θ$ vektorite $d \to s$ ja $\to r$ vahel kõikide elementide korral võrdne $90^{\circ}$ , ükskõik kus see element juhtmes ka ei paikneks. Samuti kehtib võrdus $r = R$ . Seega asendades $r$ suurusega $R$ ja võttes valemis 29-1 nurga $θ$ võrdseks $90^{\circ}$ , saame

(29-8)

d B = \frac{μ_{0}}{4 π} \frac{i d s sin 90^{\circ}}{R^{2}} = d B = \frac{μ_{0}}{4 π} \frac{i d s}{R^{2}}

Poolkaare iga voolu-pikkuse element tekitab punktis $C$ sellise suurusega magnetvälja. Parema käe reegli rakendamine mistahes punktis piki juhet (nagu joonisel 29-6c) näitab, et kõik diferentsiaalsed magnetväljad $d \to B$ on punktis $C$ sama suunaga, otse lehekülje tasandist välja. Seega on summaarne magnetväli punktis $C$ lihtsalt kõikide diferentsiaalsete magnetväljade $d \to B$ summa (integraal). Võrdust $d s = R d ϕ$ kasutades vahetame integraalis muutuja $d s$ muutujaga $d ϕ$ ja saame valemist 29-8

B = \int d B = \int_{0}^{ϕ} \frac{μ_{0}}{4 π} \frac{i R d ϕ}{R^{2}} = \frac{μ_{0} i}{4 π R} \int_{0}^{ϕ} d ϕ

Pärast integreerimist leiame, et

(ringkaare keskmes, 29-9)

B = \frac{μ_{0} i ϕ}{4 π R}

Märgime, et see valem annab meile magnetvälja suuruse ainult juhtmekaare keskmes. Ka on vaja meeles pidada, et nurk $ϕ$ peab olema antud radiaanides ja mitte nurgakraadides. Näiteks kui vooluga juhe on täisringi kujuline, tuleb magnetvälja leidmiseks ringi keskmes valemis 29-9 asendada nurk $ϕ$ väärtusega $2 π r a d$ , mis annab tulemuseks

(täisringi keskmes, 29-10)

B = \frac{μ_{0} i (2 π)}{4 π R} = \frac{μ_{0} i}{2 R}

Ajutegevusega kaasnev magnetväli

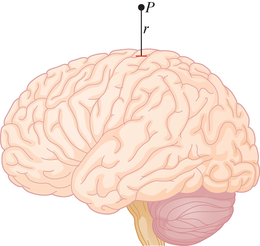
Teadlased, meedikud ja psühholoogid tahaksid mõista, kuidas funktsioneerib inimaju. Üheks nende töömeetodiks on magnetoentsefalograafia (MEG) - protseduur, milles jälgitakse inimaju magnetvälja ajal, mil inimene sooritab teatud tegevusi, nagu näiteks sõnade lugemine. See tegevus aktiveerib teatud piirkonna ajus, näiteks lugemisega seotud piirkonna, ja põhjustab nõrku elektriimpulsse, mis saadetakse edasi mööda juhtivaid kanaleid ajurakkude vahel. Nagu igasugune vool, nii tekitavad ka ajuvoolu impulsid magnetvälja.

JOONIS 29-7 Vooluimpulss piki ajukääru lõhet aju pinnal tekitab magnetvälja punktis $P$ , mis asub impulsist kaugusel $r$ .

MEG-aparatuuriga avastatud magnetvälja tekitavad arvatavasti elektriimpulsid, mis kulgevad piki kurdusid (lõhesid) aju pinnal (joonis 29-7). Püüame kasutada valemit 29-1, et hinnata sellise magnetvälja suurust punktis $P$ , mis asub kaugusel $r = 2 c m$ vooluimpulsist. Olgu impulsi teekond aju pinnale puutujaks, nii et nurk $θ$ valemis 29-1 on $90^{\circ}$ . Tüüpilise vooluimpulsi korral ajus vool $i = 10 μ A$ ja impulsi teepikkus on umbes $1 m m$ . Eeldame, et see teepikkus on küllalt lühike selleks, et asendada see $1 m m$ pikkuse diferentsiaaliga $d s$ valemis 29-1. Siis annab valem 29-1 meile

B = \frac{(4 π \times 10^{- 7} T \cdot m / A)}{4 π} \frac{(10 \times 10^{- 6} A) (1 \times 10^{- 3} m)}{(2 \times 10^{- 2} m)^{2}} sin 90^{\circ} = 2, 5 \times 10^{- 12} T \approx 3 p T

See on väga väike magnetväli, rohkem kui miljon korda nõrgem kui Maa magnetväli aju asukohas. Seega ei piisa aju magnetvälja avastamiseks sellest, et lihtsalt hoida kompassi oma aju lähedal ja loota, et ajutegevus suudab pöörata kompassi magnetnõela. Kompassi asemel on vaja ülimalt tundlikku instrumenti, milleks on ülijuhtiv kvantinterferentsseade (SQUID) ja mis on võimeline mõõtma magnetvälju suurusega vähem kui $1 p T$ ; isegi siis tuleb võtta tarvitusele kõikvõimalikud abinõud, et kõrvaldada mõõtmispaiga lähedalt muutuvat magnetvälja tekitavad lisaallikad.

Näidisülesanne 29-1, Arenda oma oskusi

Juhet joonisel 29-8a läbib vool

i

ning juhe koosneb ringjoone kaarest raadiusega

R

, mis toetub nurgale

π / 2 r a d

, ja kahest sirgest juhtmelõigust, mille pikendused lõikuvad ringjoone kaare kõveruskeskmes

C

. Millise magnetvälja

\to B

tekitab vool punktis

C

Lahendus

JOONIS 29-8 (a) Juhe koosneb kahest sirgest osast (1 ja 2) ja ringikaarest (3) ning seda läbib vool $i$ . (b) Voolu-pikkuse elemendi jaoks võrdub osas $1$ nurk $d \to s$ ja $^r$ vahel nulliga. (c) Juhtme ringikaare kujulist osa läbiva vooluga kaasneva magnetvälja ${\to B}_{3}$ suuna määramine punktis $C$ . Magnetväli on suunatud lehekülje tasandisse.

JUHTMÕTTED Magnetvälja $\to B$ punktis $C$ saab leida Biot’- Savart’i seaduse valemist 29-3. Valemi 29-3 rakendamine on lihtsam siis, kui hinnata magnetvälja $\to B$ eraldi juhtme kolme osa jaoks: (1) sirge osa jaoks vasakul, (2) sirge osa jaoks paremal ning (3) ringjoone kaare jaoks.

Sirged osad: voolu-pikkuse suvalise elemendi jaoks osas $1$ on nurk $θ$ diferentsiaalse pikkuse $d \to s$ ja ühikvektori $^r$ vahel alati null (joonis 29-8b). Seega saame valemist
29-1

d B_{1} = \frac{μ_{0}}{4 π} \frac{i d s sin θ}{r^{2}} = \frac{i d s sin 0}{r^{2}} = 0

Järelikult ei tekita vooluga juhtme sirge osa $1$ kogu pikkuse ulatuses magnetvälja punktis $C$ ,

B_{1} = 0

Sama olukord on ka juhtme teises sirges osas $2$ , kus nurk $θ$ diferentsiaali $d \to s$ ja ühikvektori $^r$ vahel voolu-pikkuse suvalise elemendi korral on võrdne $180^{\circ}$ . Seega saame

B_{2} = 0

Ringjoone kaar: Biot’-Savarti’i seadus magnetvälja arvutamiseks ringjoone kaare kõveruskeskmes on antud valemiga 29-9 ( $B = μ_{0} i ϕ / 4 π R$ ). Meie ülesandes toetub ringjoone kaar nurgale $ϕ$ , mis on võrdne $π / 2 r a d$ . Seega annab valem 29-9 magnetvälja ${\to B}_{3}$ suuruseks kaare kõveruskeskmes $C$

B_{3} = \frac{μ_{0} i (π / 2)}{4 π R} = \frac{μ_{0} i}{8 R}

Selleks, et leida ${\to B}_{3}$ suunda, rakendame parema käe reeglit vastavalt joonisele 29-4. Haarame mõtteliselt ringjoone kaare oma parema käega vastavalt joonisele 29-8c nii, et pöidla suund ühtiks voolu suunaga juhtmes. Suund, mida siis näitavad juhtme ümber asetsevad sõrmed, ühtib magnetvälja jõujoonte suunaga ümber juhtme. Punkti $P$ ümbruses (ringjoone kaare sees) osutavad sõrmed lehekülje tasandi sisse. Seega on ${\to B}_{3}$ suunatud lehekülje tasandisse.

Summaarne magnetväli: summaarse magnetvälja leidmiseks on vaja liita kaks või rohkem magnetvälja. Kuna magnetväljad on vektorsuurused, siis tuleb leida nende vektorsumma ja mitte liita arvuliselt vaid nende suurusi. Antud juhul tekitab ainult ringikaare kujuline juhtmeosa magnetvälja punktis $C$ . Seega saame summaarse magnetvälja $\to B$ suuruseks

B = B_{1} + B_{2} + B_{3} = 0 + 0 + \frac{μ_{0} i}{8 R} = \frac{μ_{0} i}{8 R} - -- - - -- -

Magnetvälja $\to B$ suund ühtib välja ${\to B}_{3}$ suunaga, vastavalt joonisele 29-8 lehekülje tasandi sisse.

Näidisülesanne 29-2, Arenda oma oskusi

Joonisel 29-9a on näidatud kaks pikka paralleelset juhet vooludega

i_{1}

i_{2}

, mis on vastassuunalised . Milline on summaarse magnetvälja suurus ja suund punktis

P

? Lähteandmed:

i_{1} = 15 A

i_{2} = 32 A

d = 5, 3 c m

Lahendus

JOONIS 29-9 (a) Kaks juhet vooludega $i_{1}$ ja $i_{2}$ , mis on vastassuunalised (leheküljest välja ja lehekülje sisse). Paneme tähele täisnurki punktis $P$ . (b) Kahe eraldi välja ${\to B}_{1}$ ja ${\to B}_{2}$ vektorliitmine annab summaarse välja $\to B$ .

JUHTMÕTTED (1) Summaarne magnetväli $\to B$ punktis $P$ on kahte juhet läbivate voolude magnetväljade vektorsumma. (2) Suvalise voolu magnetvälja saab leida Biot’-Savart’i seadusest. Punktide jaoks, mis asuvad pikka sirget juhet läbiva voolu lähedal, annab selle seaduse rakendamine tulemuseks valemi 29-4.

Vektorite leidmine: joonisel 29-9a asub punkt $P$ kaugusel $R$ mõlemast voolust $i_{1}$ ja $i_{2}$ . Seega ütleb valem 29-4 meile, et punktis $P$ on nende voolude magnetväljad ${\to B}_{1}$ ja ${\to B}_{2}$ suurustega vastavalt

B_{1} = \frac{μ_{0} i i_{1}}{2 π R} ja B_{2} = \frac{μ_{0} i i_{2}}{2 π R}

Täisnurkses kolmnurgas joonisel 29-9a on alusnurgad (külgede $R$ ja $d$ vahel) mõlemad võrdsed $45^{\circ}$ . Seega saame kirjutada $cos 45^{\circ} = R / d$ ja asendada pikkuse $R$ avaldisega $d cos 45^{\circ}$ . Magnetväljade suurused $B_{1}$ ja $B_{2}$ avalduvad nüüd

B_{1} = \frac{μ_{0} i i_{1}}{2 π d cos 45^{\circ}} ja B_{2} = \frac{μ_{0} i i_{2}}{2 π d cos 45^{\circ}}

Tahame leida ${\to B}_{1}$ ja ${\to B}_{2}$ vektorsumma, mis on summaarne magnetväli $\to B$ punktis $P$ . Selleks, et leida ${\to B}_{1}$ ja ${\to B}_{2}$ suundi, rakendame joonisel 29-4 toodud parema käe reeglit mõlemale voolule joonisel 29-9a. Juhtme $1$ jaoks, milles vool on suunatud lehekülje tasandist välja, haarame mõtteliselt juhtme oma paremasse kätte nii, et pöial osutaks lehekülje tasandist välja. Siis näitavad kõverdunud sõrmed, et magnetvälja jõujooned kulgevad vastu kellaosuti liikumise suunda. Punkti $P$ ümbruses on need suunatud üles ja vasakule. Meenutame, et magnetväli pikka sirget juhet läbiva voolu lähedal peab olema suunatud risti radiaalse sirgega, mis ühendab antud punkti ja voolu. Seega peab ${\to B}_{1}$ olema suunatud üles ja vasakule, nagu on näidatud joonisel 29-9b. (Paneme tähele, et punkti $P$ ja juhet $1$ ühendava sirge ning vektori ${\to B}_{1}$ vahel on täisnurga märk.)

Korrates eelnevat arutlust voolu jaoks juhtmes $2$ , leiame, et ${\to B}_{2}$ on suunatud üles ja paremale vastavalt joonisele 29-9b. (Punkti $P$ ja juhet $2$ ühendava sirge ning vektori ${\to B}_{2}$ vahel on samuti täisnurga märk.)

Vektorite liitmine: nüüd saame magnetvälja $\to B$ leidmiseks liita ${\to B}_{1}$ ja ${\to B}_{2}$ vektoriaalselt punktis $P$ , kasutades kas vektorarvutust võimaldavat kalkulaatorit või lahutades vektorid komponentideks ja need siis liites, et saada $\to B$ . Kuid joonisel 29-9b on toodud veel kolmas meetod: kuna vektorid ${\to B}_{1}$ ja ${\to B}_{2}$ on teineteisega risti, siis on need täisnurkse kolmnurga kaatetid, kus hüpotenuusiks on $\to B$ . Pythagorase teoreem annab meile seega

B = \sqrt{B_{1}^{2} + B_{2}^{2}} = \frac{μ_{0}}{2 π d (cos 45^{\circ})} \sqrt{i_{1}^{2} + i_{2}^{2}} = \frac{(4 π \times 10^{- 7} T \cdot m / A) \sqrt{(15 A)^{2} + (32 A)^{2}}}{(2 π) (5, 3 \times 10^{- 2} m) (cos 45^{\circ})} = 1, 89 \times 10^{- 4} T \approx 190 μ T - ------ - - ------ -

Nurk $ϕ$ vektorite $\to B$ ja ${\to B}_{2}$ vahel joonisel 29-9b on leitav seosest

ϕ = t a n^{- 1} \frac{B_{1}}{B_{2}}

mis koos $B_{1}$ ja $B_{2}$ väärtustega annab tulemuseks

ϕ = t a n^{- 1} \frac{i_{1}}{i_{2}} = t a n^{- 1} \frac{15 A}{32 A} = 25^{\circ}

Nurk magnetvälja $\to B$ ja $x$ -telje vahel vastavalt joonisele 29-9b on seega

ϕ + 45^{\circ} = 25^{\circ} + 45^{\circ} = 70^{\circ} - -- - - -- -

Ülesannete lahendamise juhised

Juhis 1: Parema käe reeglid

Selleks, et orienteeruda parema käe reeglites, mida oleme juba kasutanud (ja mida kasutame ka edaspidi), teeme neist lühikese ülevaate.

Parema käe reegel vektorkorrutise jaoks. See reegel defineeriti punktis 3-8 ja see on mõeldud vektorkorrutise suuna määramiseks. Reegli rakendamiseks on vaja suunata oma parema käe sõrmed nii, et need pööravad vektorkorrutise esimest vektorit teise vektori poole ümber vektorite vahelise väiksema nurga. Siis näitab väljasirutatud pöial vektorkorrutise suunda. Seda reeglit kasutasime 11. peatükis selleks, et leida jõumomendi ja pöörlemishulga vektoreid; 28. peatükis kasutasime seda selleks, et leida magnetväljas asuvale vooluga juhtmele mõjuva magnetjõu suunda.

Magnetismiga seotud kõver-sirge parema käe reeglid. Paljudes olukordades, kaasa arvatud magnetismi uurimisel, on otstarbekas ühendada „kõver“ element ja „sirge“ element. Seda saab teha oma parema käe (kõverdatud) sõrmede ja (sirge) pöidla abil. Võtame näiteks punktis 28-9 toodud juhu, kus ühendasime voolu silmuses (kõver element) silmuse normaalivektoriga $\to n$ (sirge element): kui kõverdad oma parema käe sõrmed ümber silmuse voolu suunas, siis Sinu väljasirutatud pöial näitab normaalivektori $\to n$ suunda. See on ühtlasi ka silmuse magnetilise dipoolmomendi $\to μ$ suund.

Selles punktis tutvustasime teist magnetismiga seotud kõver-sirge parema käe reeglit. Selleks, et määrata magnetvälja jõujoonte suunda ümber voolu-pikkuse elemendi, on vaja suunata parema käe väljasirutatud pöial voolu suunas. Siis sõrmed painduvad loomulikul viisil ümber voolu-pikkuse elemendi magnetvälja jõujoonte suunas, mis asetsevad ümber antud elemendi.

Jõud kahe paralleelse voolu vahel

Kaks pikka vooluga juhet mõjuvad teineteisele jõuga. Joonisel 29-10 on näidatud kaks sellist juhet, mis asuvad teineteisest kaugusel $d$ , ning neid läbivad voolud $i_{a}$ ja $i_{b}$ . Leiame juhtmete vastastikusest mõjust tingitud jõud.

JOONIS 29-10 Kaks paralleelset samasuunalise vooluga juhet tõmbuvad omavahel. Siin ${\to B}_{a}$ on magnetväli juhtme $b$ ümbruses, mille on tekitanud vooluga juhe $a$ , ja ${\to F}_{b a}$ on resultantjõud, mis mõjub juhtmele $b$ , sest seda läbiv vool asub magnetväljas ${\to B}_{a}$ .

Leiame kõigepealt juhtmele $b$ joonisel 29-10 mõjuva jõu, mis on tingitud voolust juhtmes $a$ . Selle voolu magnetväli ${\to B}_{a}$ on otsitava jõu vahetu tekitaja. Selleks, et leida jõudu, on vaja teada magnetvälja ${\to B}_{a}$ suurust ja suunda juhtme $b$ asukohas. Välja ${\to B}_{a}$ suurus juhtme $b$ igas punktis on leitav valemi 29-4 põhjal:

(29-11)

B_{a} = \frac{μ_{0} i_{a}}{2 π d}

Kõvera-sirge parema käe reegel ütleb meile, et väli ${\to B}_{a}$ juhtme $b$ ümbruses on suunatud alla, nagu on näha ka joonisel 29-10.

Kui magnetväli on teada, siis saab arvutada ka jõu, mida see väli avaldab juhtmele $b$ . Valem 28-26 ütleb meile, et välise magnetvälja ${\to B}_{a}$ poolt tekitatud jõud ${\to F}_{b a}$ , mis mõjub juhtme $b$ osale pikkusega $L$ , avaldub kujul

(29-12)

{\to F}_{b a} = i_{b} \to L \times {\to B}_{a}

kus $L$ on juhtme pikkusvektor. Joonisel 29-10 on vektorid $\to L$ ja ${\to B}_{a}$ teineteisega risti, seega saame valemi 29-11 abil

(29-13)

F_{b a} = i_{b} L B_{a} sin 90^{\circ} = \frac{μ_{0} L i_{a} i_{b}}{2 π d}

Jõu ${\to F}_{b a}$ suund ühtib vektorkorrutise $\to L \times {\to B}_{a}$ suunaga. Rakendades $\to L$ ja ${\to B}_{a}$ vektorkorrutisele parema käe reeglit näeme, et jõud Fba on suunatud otse juhtme a poole, nagu on näha ka joonisel 29-10.

Üldine protseduur vooluga juhtmele mõjuva jõu arvutamiseks on järgmine:

selleks, et leida vooluga juhtmele teise vooluga juhtme poolt rakendatud jõud, on vaja esmalt leida teise juhtme magnetväli esimese juhtme ümbruses. Siis tuleb leida esimesele juhtmele mõjuv jõud, mida see magnetväli tekitab.

Nüüd võiksime kasutada seda protseduuri juhtmele $a$ mõjuva jõu arvutamiseks, mis on tingitud voolust juhtmes $b$ . Veenduksime, et leitud jõud on suunatud juhtme $b$ suunas ja seetõttu tõmbuvad kaks paralleelset juhet samasuunaliste (paralleelsete) vooludega teineteise suunas. Analoogselt: kui kahes paralleelses juhtmes on voolud vastassuunalised, siis need kaks juhet tõukuvad teineteisest.

Samasuunalised voolud tõmbuvad teineteise suunas ja vastassuunalised voolud tõukuvad teineteisest.

Paralleelsete voolude vahel valitsev jõud on aluseks ampri definitsioonile (amper on üheks seitsmest SI süsteemi põhiühikust). See definitsioon, mis võeti vastu juba 1946. aastal, on järgmine:

Amper on selline konstantne vool, mis kahte teineteisest vaakumis $1$ meetri kaugusel asetsevat lõpmata pikka väga väikese ristlõikega sirget paralleelset juhet läbides tekitab nende vahel jõu $2 \times 10^{- 7}$ njuutonit juhtme pikkuse meetri kohta.

Relsskahur

Üheks valemiga 29-13 väljendatud füüsikalise nähtuse rakenduseks on relsskahur (ingl rail gun). Selles seadmes kiirendab magnetjõud mürsu lühikese aja jooksul suure kiiruseni. Relss-kahuri põhimõtet selgitab joonis 29-11a. Tugev vool saadetakse piki ühte kahest paralleelsest juhtivast relsist läbi relssidevahelise kitsa vaskriba (mis toimib nagu sulavkaitse) ja siis tagasi vooluallikasse piki teist relssi. Väljalennutatav mürsk asub kaitsme taga ja on relsside vahel (hõõrdevabalt) paigal. Vahetult pärast seda, kui relssidesse lastakse vool, hakkab vaskriba sulama ja aurustuma, tekitades kaitsme asukohas relsside vahel elektrit juhtiva gaasi.

Kõver-sirge parema käe reegel joonisel 29-4 näitab, et voolud relssides joonisel 29-11a tekitavad magnetvälja, mis on suunatud relsside vahel allapoole. Summaarne magnetväli $\to B$ mõjutab tekkinud gaasi jõuga $\to F$ tänu gaasi läbivale voolule $i$ (joonis 29-11b). Valemist 29-12 ja parema käe reeglist vektorkorrutise jaoks järeldub, et $\to F$ on suunaga eemale piki relsse. Kuna gaasi rõhutakse eemale piki relsse, siis tõukab see mürsku, andes sellele kiirenduse kuni $5 \times 10^{6} g$ ja lennutab selle relssidelt välja kiirusega $10 k m / s$ , kusjuures kõik see toimub umbes $1$ millisekundi jooksul. Kunagi tulevikus võivad sellised relss-kahurid leida kasutust materjalide saatmiseks kosmosesse kaevetöödelt Kuul või asteroidil.

KONTROLLKÜSIMUS 1

Siin toodud joonisel on näidatud kolm pikka sirget paralleelset üksteisest võrdsel kaugusel asetsevat vooluga juhet koos võrdsete voolude ja suundadega kas lehekülje tasandi sisse või sellest välja. Reasta juhtmed vastavalt neile mõjuva jõu suuruse järgi, mis tekitatakse teistes juhtmetes olevate voolude poolt, alustades suurimast.

Answer

Ampère’i seadus

Summaarset elektrivälja, mis on tekitatud suvalise laengujaotuse poolt, saab leida nii, et esmalt leiame laenguelemendi diferentsiaalse elektrivälja $d \to E$ ja siis summeerime kõik diferentsiaalsed elektriväljad $d \to E$ . Keerulise laengujaotuse korral on summaarse elektrivälja leidmiseks arvatavasti vaja kasutada arvuti abi. Kuid kui laengujaotus on tasandilise, silindrilise või sfäärilise sümmeetriaga, saab Gaussi seaduse abil leida elektrivälja oluliselt väiksema vaevaga.

JOONIS 29-13 Parema käe reegel Ampère’i seaduse jaoks määrab Ampère’i silmusega ümbritsetud voolude suunad. Joonisel esitatud olukord on sama kui joonisel 29-12.

Samamoodi on võimalik leida summaarne magnetväli, mis on tekitatud suvalise voolude jaotuse poolt nii, et esmalt leiame voolu-pikkuse elemendi diferentsiaalse magnetvälja (valem 29-3) ja siis summeerime kõikide voolu-pikkuse elementide diferentsiaalsed magnetväljad $d \to E$ . Ka siin on arvatavasti vaja kasutada arvuti abi, kui voolude jaotus on keeruline. Kuid kui voolude jaotusel on mõni sümmeetria, saab magnetvälja leidmist hõlbustada, kasutades Ampère’i seadust. See seadus,
mida saab tuletada Biot’-Savart’i seadusest, on traditsiooniliselt omistatud André-Marie Ampère’ile (1775 – 1836), kelle nime kannab ka vooluühik SI süsteemis. Kuid tegelikult sõnastas selle seaduse Inglise füüsik James Clerk Maxwell. Ampère’i seadust väljendab valem

(Ampère’i seadus, 29-14)

\oint \to B \cdot d \to s = μ_{0} i_{k i n n i n e}

Silmus integraali märgil tähendab seda, et skalaarkorrutist $\to B \cdot d \to s$ tuleb integreerida üle kinnise kontuuri, mis kannab Ampère’i silmuse nime. Vool $i_{k i n n i n e}$ on summaarne vool, mis on ümbritsetud selle kinnise silmusega.

Selleks, et saada aru skalaarkorrutise $\to B \cdot d \to s$ ja selle integraali tähendusest, rakendame esmalt Ampère’i seadust üldisele situatsioonile joonisel 29-12. Joonisel on näidatud kolme pika sirge juhtme ristlõiked, mida läbivad vastavalt voolud $i_{1}$ , $i_{2}$ ja $i_{3}$ , mis on suunatud kas otse lehekülje tasandist välja või otse lehekülje tasandisse. Üks Ampère’i silmus, mis asub lehekülje tasandis, ümbritseb kahte neist vooludest, kuid mitte kolmandat. Silmusel tähistatud kellaosutile vastupidine liikumise suund näitab suvaliselt valitud integreerimissuunda valemis 29-14.

Selleks, et rakendada Ampère’i seadust, jagame mõtteliselt silmuse vektorelementideks $d \to s$ , mis on kõikjal suunatud mööda silmuse puutujaid integreerimise suunas. Oletame, et joonisel 29-12 näidatud elemendi $d \to s$ asukohas on kolme voolu summaarne magnetväli $\to B$ . Kuna juhtmed on lehekülje tasandiga risti, siis teame, et nende magnetväli $d \to s$ asukohas on joonisel 29-12 lehekülje tasandis ja seega peab ka summaarne magnetväli $\to B$ olema $d \to s$ asukohas lehekülje tasandis.

Kuid me ei tea magnetvälja suunda lehekülje tasandis. Joonisel 29-12 on $\to B$ joonestatud suvalise nurga $θ$ all vektori $d \to s$ suhtes.

Skalaarkorrutis $\to B \cdot d \to s$ valemi 29-14 vasakul poolel on võrdne korrutisega $B cos θ d s$ . Seega saab Ampère’i seaduse avaldada kujul

(29-15)

\oint \to B \cdot d \to s = \oint B cos θ d s = μ_{0} i_{k i n n i n e}

Nüüd võib skalaarkorrutist $\to B \cdot d \to s$ tõlgendada kui Ampère’i silmuse elemendi $d s$ korrutist magnetvälja komponendiga $B cos θ$ , mis on silmuse puutuja suunas. Integreerimist võib siis tõlgendada kui kõikide selliste korrutiste summeerimist üle kogu silmuse.

Tegelikul integreerimisel ei ole enne vaja teada $\to B$ suunda. Võime meelevaldselt eeldada, et $\to B$ suund ühtib ligilähedaselt integreerimissuunaga (nagu ka joonisel 29-12). Seejärel kasutame kõver-sirge parema käe reeglit selleks, et omistada kas pluss- või miinusmärk kõikidele vooludele, mis kokku annavad silmuse poolt ümbritsetud summaarse voolu $i_{k i n n i n e}$ :

kõverda oma parem käsi ümber Ampère’i silmuse nii, et sõrmed näitavad integreerimissuunda. Silmuse poolt ümbritsetud voolule omistatakse plussmärk, kui see on väljasirutatud pöidla suunas, ja miinusmärk, kui see on vastassuunas.

Lõpuks leiame valemist 29-15 magnetvälja $\to B$ suuruse. Kui $B$ osutub positiivseks, siis oli meie poolt oletatud $\to B$ suund õige. Kui see osutub aga negatiivseks, siis võime miinusmärgi ära jätta, kui muudame joonisel $\to B$ suuna vastupidiseks.

Joonisel 29-13 on näidatud kõver-sirge parema käe reegel, mida on vaja kasutada joonisel 29-12 antud olukorra uurimisel Ampère’i seaduse abil. Integreerides kellaosuti liikumisele vastupidises suunas, saame silmusega ümbritsetud summaarse voolu

I_{k i n n i n e} = i_{1} - i_{2}

(Vool $i_{3}$ ei ole silmusega ümbritsetud.) Nüüd saame valemi 29-15 kirjutada kujul

(29-16)

\oint B cos θ d s = μ_{0} (i_{1} - i_{2})

Võib küsida, miks vool $i_{3}$ , mis on osaline valemi 29-16 vasakul poolel oleva magnetvälja $B$ tekitamisel, ei esine valemi paremal poolel. Vastus on, et voolu $i_{3}$ panus magnetvälja tekitamisse koondub välja, sest valemis 29-16 integreeritakse üle kogu silmuse. Erinevalt sellest ei koondu välja silmusega ümbritsetud voolude panused magnetvälja tekitamisse.

Valemist 29-16 ei saa leida magnetvälja suurust $B$ , sest joonisel 29-12 kujutatud olukorra jaoks ei ole piisavalt informatsiooni integraali lihtsustamiseks ja arvutamiseks. Kuid me teame integreerimise tulemust, mis peab olema võrdne $μ_{0} (i_{1} - i_{2})$ , sest see on silmust läbiv summaarne vool.

Rakendame nüüd Ampère’i seadust kahes olukorras, kus sümmeetria laseb meil integraali lihtsustada ja välja arvutada ning sel viisil magnetvälja leida.

Magnetväli väljaspool pikka sirget vooluga juhet

Joonisel 29-14 on näidatud pikk sirge juhe, mida läbib vool $i$ suunaga otse lehekülje tasandist välja. Valem 29-4 ütleb meile, et voolu magnetväli $\to B$ on võrdse suurusega kõikides punktides, mis asuvad juhtmest ühel ja samal kaugusel $r$ . See tähendab seda, et magnetväli $\to B$ on juhtme suhtes silindrilise sümmeetriaga. Seda sümmeetriat võime kasutada selleks, et lihtsustada integrandi Ampère’i seaduses (valemid 29-14 ja 29-15), kui ümbritseme juhtme kontsentrilise ringjoonelise Ampère’i silmusega, mille raadius on $r$ nagu näidatud joonisel 29-14. Magnetväli $\to B$ on siis silmuse igas punktis võrdse suurusega $B$ . Integreerime kellaosuti liikumisele vastassuunas, nii et $d \to s$ on joonisel 29-14 näidatud suunas.

JOONIS 29-14 Ampère’i seaduse kasutamine magnetvälja leidmiseks vooluga $i$ pika sirge ringikujulise ristlõikega juhtme ümber. Ampère’i silmus on kontsentriline ringjoon, mis on juhtmest väljaspool.

Avaldist $B cos θ$ valemis 29-15 saab veelgi lihtsustada, kui paneme tähele, et nii $\to B$ kui ka $d \to s$ on silmuse igas punktis silmuse puutuja sihis. Seega on $\to B$ ja $d \to s$ silmuse igas punktis kas samasuunalised või vastassuunalised; oletame meelevaldselt, et õige on neist esimene. Siis on igas punktis nurk $θ$ suuruste $d \to s$ ja $\to B$ vahel võrdne nulliga ja $cos θ = cos 0^{\circ} = 1$ . Integraal valemis 29-15 võrdub

\oint \to B \cdot d \to s = \oint B cos θ d s = B \oint d s = B (2 π r)

Paneme tähele, et $\oint d s$ on kõikide pikkusega $d s$ elementide summa üle kogu ringjoonelise
silmuse, s.t see on lihtsalt silmuse ümbermõõt $2 π r$ .

Parema käe reegel ütleb, et joonisel 29-14 näidatud vool on positiivne. Ampère’i seaduse parem pool omandab kuju $+ μ_{0} i$ ja seega saame

B (2 π r) = μ_{0} i

või

(sirge juhtme ümber, 29-17)

B = \frac{μ_{0} i}{2 π r}

Veidi tähistusi muutes näeme, et oleme saanud valemi 29-4, mille tuletasime juba varem tunduvalt suurema vaevaga, kasutades Biot’-Savart’i seadust. Lisaks teame, et kuna magnetvälja suurus $B$ osutus positiivseks, siis peab $\to B$ õige suund ühtima joonisel 29-14 näidatud suunaga.

Magnetväli pika sirge vooluga juhtme sees

JOONIS 29-15 Ampère’i seaduse kasutamine voolu $i$ magnetvälja leidmiseks pika sirge ringikujulise ristlõikega juhtme sees. Vool on kogu juhtme ristlõike ulatuses ühtlaselt jaotatud ja see on suunatud lehekülje tasandist välja. Juhtme sisse on joonistatud Ampère’i silmus.

Joonisel 29-15 on näidatud raadiusega $R$ pika sirge juhtme ristlõige, juhtmes kulgeb ühtlaselt jaotatud vool $i$ otse joonise tasandist välja. Kuna vool on juhtme ristlõike ulatuses ühtlaselt jaotatud, siis peab voolu magnetväli $\to B$ olema silindrilise sümmeetriaga. Selleks, et leida magnetväli juhtme sees asuvates punktides, võime jälle kasutada Ampère’i silmust raadiusega $r$ vastavalt joonisele 29-15, kuid nüüd kehtib $r < R$ . Sümmeetria veenab meid, et $\to B$ on taas silmuse puutuja sihis, nagu näha ka jooniselt, ja seetõttu Ampère’i seaduse vasak pool annab jälle

(29-18)

\oint \to B \cdot d \to s = B \oint d s = B (2 π r)

Selleks, et leida Ampere’i seaduse parem pool, paneme tähele, et kuna vool on ühtlaselt jaotatud, siis $i_{k i n n i n e}$ , mis on ümbritsetud silmusega, on võrdeline silmusega haaratud pinnaga. Seega saame

(29-19)

i_{k i n n i n e} = i \frac{π r^{2}}{π R^{2}}

Parema käe reegel ütleb meile, et $i_{k i n n i n e}$ on positiivne. Seega Ampère’i seadus annab

B (2 π r) = μ_{0} i \frac{π r^{2}}{π R^{2}}

või

(sirge juhtme sees, 29-20)

B = (\frac{μ_{0} i}{2 π R^{2}}) r

Seega on juhtme sees magnetvälja suurus $B$ võrdeline radiaalkaugusega $r$ . See tähendab, et juhtme keskmes on magnetvälja suurus võrdne nulliga ja saavutab maksimaalse väärtuse juhtme pinnal, kus $r = R$ . Paneme tähele, et valemid 29-17 ja 29-20 annavad ühesuguse väärtuse magnetvälja suuruse $B$ jaoks juhul, kui $r = R$ . See tähendab, et valemid magnetvälja jaoks juhtmest väljaspool ja juhtme sees annavad välja suuruse jaoks juhtme pinnal võrdse tulemuse.

KONTROLLKÜSIMUS 2

Siinsel joonisel on näidatud kolm võrdset voolu

i

(kaks neist on samasuunalised ja üks vastassuunaline) ja neli Ampère’i silmust. Reasta silmused vastavalt integraali

\oint \to B \cdot d \to s

väärtusele üle juhtmete, alustades suurimast.

Answer

Näidisülesanne 29-3

Joonisel 29-16a on näidatud pikk juhtiv silinder, mille siseraadius

a = 2, 0 c m

ja välisraadius

b = 4, 0 c m

. Silindrit läbib vool suunaga lehekülje tasandist välja ja voolutiheduse väärtus juhtme ristlõikes on antud valemiga

J = c r^{2}

, kus

c = 3, 0 \times 10^{6} A / m^{4}

r

on mõõdetud meetrites. Milline on magnetväli

\to B

punktis, mis asub kaugusel

3, 0 c m

silindri keskteljest?

Lahendus

Joonis 29-16 (a) Juhtiva silindri ristlõige, mille siseraadius on $a$ ja välisraadius $b$ . (b) On lisatud Ampère’i silmus raadiusega $r$ , et arvutada magnetväli punktides, mis asuvad silindri keskteljest kaugusel $r$ .

JUHTMÕTTED Punkt, milles tahame $\to B$ määrata, asub juhtiva silindri materjali sees, silindri sise- ja välisraadiuste vahel. Paneme tähele, et voolujaotus on silindersümmeetriline (vool on ühesugune ristlõike kõigis punktides, mis asuvad suvalisel kuid võrdsel kaugusel silindri keskteljest). Seega lubab sümmeetria kasutada Ampère’i seadust selleks, et leida $\to B$ meid huvitavas punktis. Esmalt joonistame Ampère’i silmuse vastavalt joonisele 29-16b. Silmus on kontsentriline silinder raadiusega $r = 3, 0 c m$ , sest tahame määrata $\to B$ just sellel kaugusel silindri keskteljest.

Edasi peame arvutama voolu $i_{k i n n i n e}$ , mis on ümbritsetud Ampère’i silmusega. Kuid siin ei ole vool võrdeline kaugusega nagu valemis 29-19, sest siin ei ole vool ühtlaselt jaotatud. Selle asemel järgime näidisülesandes 26-2b toodud protseduuri ja integreerime voolutiheduse suurust silindri siseraadiusest $a$ kuni silmuse raadiuseni $r$ .

Arvutused: kirjutame integraali kujul

i_{k i n n i n e} = \int J d A = \int_{a}^{r} c r^{2} (2 π r d r) = 2 π c \int_{a}^{r} r^{3} d r = 2 π c {[\frac{r^{4}}{4}]}_{a}^{r} = \frac{π c (r^{4} - a^{4})}{2}

Joonisel 29-16b näidatud (meelevaldne) integreerimissuund ühtib kellaosuti liikumise suunaga. Rakendame Ampère’i seaduse parema käe reeglit silmusele ja leiame, et vool $i_{k i n n i n e}$ tuleb võtta negatiivne, sest vool on suunatud lehekülje tasandist välja, kuid meie pöial on suunatud lehekülje tasandisse.

Järgnevalt arvutame Ampère’i seaduse vasaku poole niisamuti, nagu tegime joonisel 29-15, ning jälle saame tulemuseks valemi 29-18. Seega Ampère’i seadus

\oint \to B \cdot d \to s = μ_{0} i_{k i n n i n e}

annab meile tulemuseks

B (2 π r) = - \frac{μ_{0} π c}{2} (r^{4} - a^{4})

Avaldame siit $B$ ja paneme sisse teadaolevad andmed, saame

B = - \frac{μ_{0} c}{4 r} (r^{4} - a^{4}) = \frac{(4 π \times 10^{- 7} T \cdot m / A) (3, 0 \times 10^{6} A / m^{4})}{4 (0, 030 m)} \times [(0, 030 m)^{4} - (0, 020 m)^{4}] = - 2, 0 \times 10^{- 5} T

Seega magnetväli B punktis, mis asub 3,0 cm kaugusel keskteljest, on suurusega

B = 2, 0 \times 10^{- 5} T - ------------ - - ------------ -

ja magnetvälja jõujooned on suunatud integreerimisteele vastupidi, seega joonisel 29-16b kellaosuti liikumisele vastassuunas.

Solenoidid ja toroidid

Solenoidi magnetväli

Vaatleme veel üht olukorda, kus Ampère’i seadus kasulikuks osutub. See puudutab magnetvälja, mille tekitab vool pikas tihedalt keritud spiraalses juhtmepoolis. Sellist pooli nimetatakse solenoidiks (joonis 29-17). Eeldame, et solenoidi pikkus on palju suurem kui selle diameeter.

Joonisel 29-18 on näidatud solenoidi osa läbilõige väljavenitatud mõõtkavas. Solenoidi magnetväli võrdub solenoidi üksikute keerdude magnetväljade vektorsummaga. Punktides, mis asuvad keerule väga lähedal, käitub juhe magnetiliselt peaaegu nagu pikk sirge juhe ja magnetvälja $\to B$ jõujooned on seal peaaegu kontsentrilised ringjooned. Joonis 29-18 näitab, et kahe kõrvutise keeru magnetväljad püüavad teineteist vastamisi kustutada. Joonis näitab ka seda, et punktides, mis asuvad solenoidi sees ja juhtmest küllalt kaugel, on $\to B$ ligikaudu paralleelne solenoidi keskteljega. Ideaalses solenoidis, mille pikkus läheneb lõpmatusele ja mille ruudukujulise ristlõikega juhtmest keerud on tihedalt pakitud, on magnetväli pooli sees ühtlane ja solenoidi teljega paralleelne.

JOONIS 29-18 „Väljavenitatud“ solenoidi ristlõige läbi kesktelje. On näidatud viie keeru siinpoolsed osad ja nendes keerdudes olevate voolude magnetväljade jõujooned. Iga keeru ümber on ringjoonelised magnetvälja jõujooned. Solenoidi telje lähedal liituvad magnetvälja jõujooned summaarseks magnetväljaks, mis on suunatud piki solenoidi telge. Tihedalt asetsevad jõujooned solenoidi sees näitavad, et seal on magnetväli suur. Väljaspool solenoidi paiknevad magnetvälja jõujooned hõredalt ja seal on magnetväli väga nõrk.

Punktides solenoidi kohal, nagu näiteks punkt $P$ joonisel 29-18, on solenoidi keerdude ülemiste poolte (ülemised pooled on joonisel tähistatud nooleotsa märgiga $⊙$ ) magnetväljad suunatud vasakule (nagu näitavad ka jõujooned $P$ lähedal) ning püüavad kustutada magnetvälju, mille tekitavad keerdude alumised pooled (alumised pooled on joonisel tähistatud noolesaba märgiga $\otimes$ ) ja mis on suunatud paremale (joonisel pole neid näidatud). Ideaalse solenoidi piirjuhul on magnetväli väljaspool solenoidi võrdne nulliga. Ka reaalse solenoidi korral on välise magnetvälja võtmine võrdseks nulliga hea lähendus siis, kui solenoidi pikkus on palju suurem kui selle diameeter ja kui vaadelda punkte nagu $P$ , mis on väljaspool solenoidi ja kaugel sellea otstest. Magnetvälja suund piki solenoidi telge on antud kõver-sirge parema käe reegliga: kui haarata parema käega solenoid nii, et kõverdatud sõrmed järgivad voolu suunda mähises, siis osutab väljasirutatud pöial teljel oleva magnetvälja suunas.

JOONIS 29-19 Magnetvälja jõujooned lõpliku pikkusega reaalse solenoidi korral. Magnetväli on suur ja ühtlane solenoidi sisepunktides nagu $P_{1}$ , kuid suhteliselt nõrk väljaspool asuvates punktides nagu $P_{2}$ .

Joonisel 29-19 on näidatud magnetvälja $\to B$ jõujooned reaalse solenoidi korral. Jõujoonte asetus solenoidi sees näitab, et magnetväli on seal üsna suur ja ühtlane pooli kogu ristlõike ulatuses. Magnetväli solenoidist väljaspool on aga suhteliselt nõrk.

Rakendame nüüd Ampère’i seadust

(29-21)

\oint \to B \cdot d \to s = μ_{0} i_{k i n n i n e}

ideaalsele solenoidile joonisel 29-20, kus $\to B$ on ühtlane solenoidi sees ja võrdne nulliga väljaspool solenoidi, kasutades nelinurkset Ampère’i silmust $a b c d a$ . Kirjutame $\oint \to B \cdot d \to s$ nelja integraali summana, kus igale integraalile vastab silmuse külg:

(29-22)

\oint \to B \cdot d \to s = \int_{a}^{b} \to B \cdot d \to s + \int_{b}^{c} \to B \cdot d \to s + \int_{c}^{d} \to B \cdot d \to s + \int_{d}^{a} \to B \cdot d \to s

JOONIS 29-20 Ampère’i seaduse rakendamine pika ideaalse vooluga $i$ solenoidi osale. Ampère’i silmus on nelinurk abcda.

Esimene integraal valemi 29-22 paremal poolel on $B h$ , kus $B$ on ühtlase magnetvälja $\to B$ suurus $B$ solenoidi sees ja $h$ on külje (suvaline) pikkus punktist $a$ punktini $b$ . Teine ja neljas integraal võrduvad nulliga, sest nende külgede igas punktis on diferentsiaal $d s$ kas magnetväljaga $\to B$ risti või on magnetväli võrdne nulliga ja seetõttu on korrutis $\to B \cdot d \to s$ võrdne nulliga. Kolmas integraal, kus integreeritakse üle väljaspool solenoidi oleva külje, on võrdne nulliga, sest $B = 0$ kõikjal väljaspool solenoidi. Seega $\to B \cdot d \to s$ üle kogu nelinurkse silmuse võrdub korrutisega $B h$ .

Summaarne vool $i_{k i n n i n e}$ , mis on ümbritsetud nelinurkse Ampère’i silmusega joonisel 29-20, ei ole võrdne vooluga i solenoidi mähises, sest mähise keerud läbivad silmust rohkem kui üks kord. Olgu $n$ keerdude arv pikkusühiku kohta solenoidis, siis on silmusega haaratud keerdude arv $n h$ ja

I_{k i n n i n e} = i (n h)

Ampère’i seadus annab meile nüüd

B h = μ_{0} i n h

või

(ideaalne solenoid, 29-23)

B = μ_{0} i n

Kuigi tuletasime valemi 29-23 lõpmata pika ideaalse solenoidi jaoks, kehtib see küllalt hästi ka reaalsete solenoidide korral, kui rakendada seda ainult solenoidide sisepunktides ja piisavalt kaugel solenoidi otstest. Valem 29-23 on kooskõlas katsetega, mis näitavad, et magnetvälja suurus $B$ solenoidi sees ei sõltu ei solenoidi diameetrist ega selle pikkusest ja et $B$ on ühtlane üle kogu solenoidi ristlõike. Seega annab solenoid meile praktilise võimaluse ühtlase magnetvälja leidmiseks, nii nagu paralleelplaatidega kondensaator annab praktilise võimaluse ühtlase elektrivälja
leidmiseks.

Toroidi magnetväli

Joonisel 29-21a on näidatud toroid, mis on saadud solenoidi painutamisel nii, et selle kaks otsa ühtivad, moodustades õõnsa käevõru moodi keha. Milline on magnetväli $\to B$ toroidi sees (käevõru õõnsuses)? Selle leidmiseks kasutame Ampère’i seadust ja „käevõru“ sümmeetriat.

Joonis 29-21 (a) Toroid vooluga $i$ . (b) Toroidi horisontaalne ristlõige. Sisemine magnetväli (toroidi õõnsuses) on leitav, kui rakendada Ampère’i seadust joonisel näidatud Ampère’i silmusele.

Sümmeetriast järeldub, et magnetvälja $\to B$ jõujooned toroidi sees on kontsentrilised ringid, suunatud vastavalt joonisele 29-21b. Valime Ampère’i silmuseks kontsentrilise ringi raadiusega $r$ ning liigume piki seda kellaosuti liikumise suunas. Ampère’i seadus (valem 29-14) annab meile

(B) (2 π r) = μ_{0} i N

kus $i$ on vool toroidi keerdudes (ja on positiivne keerdude nendes osades, mis on ümbritsetud Ampère’i silmusega) ning $N$ on keerdude koguarv. See annab

(toroid, 29-24)

B = \frac{μ_{0} i N}{2 π} \frac{1}{r}

Erinevalt olukorrast solenoidis, pole $B$ üle kogu toroidi ristlõike konstantne. Ampère’i seadust kasutades on lihtne näidata, et $B = 0$ punktide jaoks väljaspool ideaalset toroidi (s.t toroidi, mis nagu oleks valmistatud ideaalsest solenoidist).

Magnetvälja suund toroidis järgib meie kõver-sirge parema käe reeglit. Kui haarata toroid nii, et parema käe sõrmed painduvad toroidi mähises oleva voolu suunas, siis näitab sirutatud pöial magnetvälja suunda.

Vooluga pool kui magnetiline dipool

Siiani oleme vaadelnud magnetvälju, mille põhjustab vool pika sirge juhtme, solenoidi ja toroidi ümbruses. Nüüd võtame vaatluse alla magnetväljad, mille tekitavad vooluga poolid. Punktis 28-10 nägime, et selline pool käitub magnetilise dipoolina selles mõttes, et kui asetame pooli välisesse magnetvälja $\to B$ , siis mõjub sellele jõumoment $\to τ$

(29-25)

\to τ = \to μ \times \to B

Siin $\to μ$ on pooli magnetiline dipoolmoment ning selle suurus on $N i A$ , kus $N$ on keerdude arv, $i$ on üksikut keerdu läbiv vool ja $A$ on pindala, mis on haaratud üksiku keeruga. (Hoiatus: ärge ajage segi magnetilist dipoolmomenti $\to μ$ magnetilise konstandiga $μ_{0}$ .)

Meenutame, et magnetilise dipoolmomendi $\to μ$ suund on antud kõver-sirge parema käe reegliga: kui haarata parema käega pool nii, et sõrmed kõverduvad selle ümber voolu suunas, siis näitab väljasirutatud pöial magnetilise dipoolmomendi $\to μ$ suunas.

Pooli magnetväli

Nüüd käsitleme vooluga pooli teist aspekti, nimelt vaatame pooli kui magnetilist dipooli. Milline on magnetväli pooli ümbritseva ruumi suvalises punktis? Selles ülesandes puudub sümmeetria, mis lubaks Ampère’i seadust kasulikult rakendada, seepärast pöördume Biot’-Savart’i seaduse poole. Lihtsuse mõttes vaatleme esmalt pooli, millel on ainult üks ringikujuline keerd, ja teeme seda ainult magnetvälja sellistes punktides, mis asuvad vertikaalsel keskteljel, mille võtame $z$ -teljeks. Näitame, et magnetvälja suurus neis punktides on

(29-26)

B (z) = \frac{μ_{0} i R^{2}}{2 (R^{2} + z^{2})^{3 / 2}}

kus $R$ on keeru raadius ning $z$ on kaugus vaadeldava punkti ja keeru keskme vahel. Magnetvälja $\to B$ suund ühtib keeru magnetilise dipoolmomendi $\to μ$ suunaga.

JOONIS 29-22 Ringvoolu magnetväli on sarnane magnetpulga magnetväljaga ja seega saab sellele omistada ka põhja- ja lõunapooluse. Ringvoolu magnetiline dipoolmoment $\to μ$ , mille suund on antud kõversirge parema käe reegliga, näitab lõunapooluselt põhjapoolusele, magnetvälja $\to B$ suunas.

Keerust kaugel asuvate teljepunktide jaoks on valemis 29-26 $z ≫ R$ . Selles lähenduses taandub valem kujule

B (z) \approx \frac{μ_{0} i R^{2}}{2 z^{3}}

Meenutades, et $π R^{2}$ on keeru pindala $A$ ja laiendades saadud tulemust $N$ keeruga poolile, võime selle valemi anda kujul

B (z) = \frac{μ_{0}}{2 π} \frac{N i A}{z^{3}}

Edasi, kuna $\to B$ ja $\to μ$ on samasuunalised, saame valemi avaldada vektorkujul, tehes ka asenduse $μ = N i A$ :

(vooluga pool, 29-27)

\to B (z) = \frac{μ_{0}}{2 π} \frac{\to μ}{z^{3}}

Seega on vooluga poolil kahesugused magnetilise dipooli omadused: (1) vooluga poolile mõjub jõumoment, kui asetada see välisesse magnetvälja; (2) vooluga pooli sees on magnetväli, mis on pooli teljel asuvate küllalt kaugete punktide jaoks antud valemiga 29-27. Joonis 29-22 näitab vooluga keeru (ringvoolu) magnetvälja, kusjuures ühel pool keerdu oleks nagu põhjapoolus (momendi $\to μ$ suunas) ja teisel pool nagu lõunapoolus; seda illustreerib ka heledalt joonistatud magnetpulk.

KONTROLLKÜSIMUS 3

Siin toodud joonisel on näidatud neli ringvoolude asetust, kus raadiustega

r

või

2 r

ringvoolude keskmed on vertikaalteljel (risti ringvooludega) ja voolud on joonisel näidatud suundades. Reasta ringvoolude asetused vastavalt summaarse magnetvälja suurusele punktis, mis asub ringvoolude vahel keskteljel, alustades suurimast.

Answer

Valemi 29-26 tõestus

Joonisel 29-23 on näidatud üks pool ringvoolu keerust, mille raadius on $R$ ja mida läbib vool $i$ . Vaatleme punkti $P$ ringvoolu keskteljel, kaugusel $z$ lehekülje tasandist. Rakendame Biot’-Savart’i seadust ringvoolu diferentsiaalsele elemendile $d s$ , mis asetseb joonisel ringvoolu vasakus otsas. Selle elemendi pikkusvektor on suunatud risti lehekülje tasandiga sellest välja. Nurk $θ$ pikkusvektori $d \to s$ ja ühikvektori $^r$ vahel joonisel 29-23 on $90^{\circ}$ . Nende kahe vektori poolt moodustatud tasand on risti lehekülje tasandiga ja sisaldab nii $^r$ kui $d \to s$ . Biot’-Savart’i seadusest (ja parema käe reeglist) tuleneb, et selle elemendi voolu diferentsiaalne magnetväli $d \to B$ punktis $P$ on nimetatud tasandiga risti ja joonise tasandis seega risti ühikvektoriga $^r$ , nagu näha joonisel 29-23.

JOONIS 29-23 Raadiusega $R$ ringvoolu ristlõige. Ringvoolu tasand on risti lehekülje tasandiga ja joonisel on näidatud vaid pool sellest. Magnetvälja leidmiseks ringvoolu vertikaalsel keskteljel asuvas punktis $P$ kasutame Biot’-Savart’i seadust.

Lahutame $d \to B$ kaheks komponendiks: $d {\to B}_{| |}$ , mis on suunaga piki ringvoolu telge, ning $d {\to B}_{⊥}$ , mis on teljega risti. Sümmeetriast järeldub, et ringjoone kõikide elementide $d s$ magnetväljade ristkomponentide $d {\to B}_{⊥}$ vektorsumma on võrdne nulliga. Seega on vaja arvestada ainult aksiaalseid komponente $d {\to B}_{| |}$ ja saame

B = \int d B_{| |}

Joonisel 29-23 toodud elementide jaoks ütleb meile Biot’-Savart’i seadus (valem 29-1), et magnetväli kaugusel $r$ avaldub kujul

d B = \frac{μ_{0}}{4 π} \frac{i d s sin 90^{\circ}}{r^{2}}

On teada ka seos

d B_{| |} = d B cos α

Ühendades need kaks valemit, saame tulemuseks

(29-28)

d B_{| |} = \frac{μ_{0} i cos α d s}{4 π r^{2}}

Joonis 29-23 näitab, et $r$ ja $α$ on teineteisest sõltuvad. Avaldame need mõlemad suurused muutuja $z$ kaudu, mis on kaugus punkti $P$ ja ringvoolu keskme vahel. Saame

(29-29)

r = \sqrt{R^{2} + z^{2}}

(29-30)

cos α = \frac{R}{r} = \frac{R}{\sqrt{R^{2} + z^{2}}}

Asendades valemid 29-29 ja 29-30 valemisse 29-28, leiame

d B_{| |} = \frac{μ_{0} i R}{4 π (R^{2} + z^{2})^{3 / 2}} d s

Kuna $i$ , $R$ ja $z$ on ühesuguse väärtusega kõikide elementide $d s$ jaoks üle kogu ringvoolu, siis integreerimine annab

B = \int d B_{| |} = \frac{μ_{0} i R}{4 π (R^{2} + z^{2})^{3 / 2}} \int d s

ehk võttes arvesse, et $\int d s$ on lihtsalt ringjoone ümbermõõt $2 π R$ , saame

B (z) = \frac{μ_{0} i R^{2}}{2 (R^{2} + z^{2})^{3 / 2}}

See on valem 29-26, mida oligi tarvis tõestada.

Summary

Vooluga juhtme magnetväli on leitav Biot’-Savart’i seadust kasutades. See seadus väidab, et voolu-pikkuse elemendi $i d \to s$ magnetväli $d \to B$ punktis $P$ , mis asub voolu-pikkuse elemendist kaugusel $r$ , on

(29-3)

d \to B = \frac{μ_{0}}{4 π} \frac{i d \to s \times^r}{r^{2}}

Siin $^r$ on ühikvektor, mis on suunatud voolu-pikkuse elemendist punkti $P$ poole. Suurus $\to μ$ , mis kannab magnetilise konstandi nime, on väärtusega $4 π \times 10^{- 7} T \cdot m/A \approx 1, 26 \times 10^{- 6} T \cdot m/A$ .

Vool $i$ ringikaares, mille raadius on $R$ ja kesknurk $ϕ$ (radiaanides), tekitab ringikaare keskmes magnetvälja suurusega

(29-9)

B = \frac{μ_{0} i ϕ}{4 π R}

Paralleelsed samasuunaliste vooludega juhtmed tõmbuvad teineteise poole ja vastassuunaliste vooludega juhtmed tõukuvad teineteisest eemale. Kummalegi juhtmele mõjub pikkusühiku $L$ kohta jõud suurusega

(29-13)

F_{a b} = i_{b} L B_{a} sin 90^{\circ} = \frac{μ_{0} L i_{a} i_{b}}{2 π d}

kus $d$ on kaugus juhtmete vahel ning $i_{a}$ ja $i_{b}$ on voolud juhtmetes.

Ampère’i seaduse kohaselt

(29-14)

\oint \to B \cdot d \to s = μ_{0} i_{kinnine}

Valemis esinev joonintegraal leitakse üle kogu kinnise silmuse, mida nimetatakse Ampère’i silmuseks. Vool $i$ valemis on silmusega ümbritsetud summaarne vool. Mõnede voolujaotuste korral on voolude magnetvälja leidmisel valem 29-14 lihtsam kui valem 29-3.

Vooluga $i$ pika solenoidi sees olevates punktides, mis asuvad kaugel solenoidi otstest, avaldub magnetvälja suurus kujul

(29-23)

B = μ_{0} i n

kus $n$ on solenoidi keerdude arv pikkusühiku kohta. Toroidi sees on magnetvälja suurus $B$ antud valemiga

(29-24)

B = \frac{μ_{0} i N}{2 π} \frac{1}{r}

kus $r$ on kaugus toroidi keskmest antud punktini.

Vooluga pool on magnetiline dipool ja selle magnetväli punktis $P$ , mis asub kaugusel $z$ piki pooli keeru tasandiga risti olevat kesktelge, on paralleelne keskteljega ja antud valemiga

(29-27)

\to B (z) = \frac{μ_{0}}{2 π} \frac{\to μ}{z^{3}}

kus $\to μ$ on pooli dipoolmoment. See valem kehtib vaid siis, kui $z$ väärtus on palju suurem kui pooli mõõtmed.

Küsimused

Joonisel 29-24 on näidatud neli olukorda, kus pikad paralleelsed juhtmed, mida läbivad risti lehekülje tasandisse või tasandist välja suunatud suuruselt võrdsed voolud, asuvad identsete ruutude nurkades. Reasta need olukorrad vastavalt summaarse magnetvälja suurusele ruudu keskmes, alates suurimast.

Answer

Joonisel 29-25 on näidatud kahe pika sirge juhtme ristlõiked. Vasakpoolne juhe kannab voolu

i_{1}

lehekülje tasandist välja. Kui juhtmetes olevate voolude summaarne magnetväli võrdub nulliga punktis

P

, siis (a) kas peab parempoolses juhtmes voolava voolu

i_{2}

suund olema suunatud lehekülje tasandist välja ning (b) kas

i_{2}

peab olema suurem, väiksem või võrdne vooluga

i_{1}

Answer

Joonisel 29-26 on näidatud kolm vooluringi, mis koosnevad sirgetest radiaalsetest lõikudest ja kontsentrilistest ringikaartest (kas pool- või veerandringid raadiustega

r

2 r

3 r

). Vooluringe läbivad võrdsed voolud. Reasta vooluringid vastavalt magnetvälja suurusele vooludega kaarte keskmes (tähistatud punktiga), alates suurimast.

Answer

Joonisel 29-27 on näidatud hetkepilt nelja elektroni kiirusvektoritest sellise juhtme läheduses, mida läbib vool

i

. Need neli kiirust on võrdse suurusega ja kiirus

{\to v}_{2}

on suunatud lehekülje tasandi sisse. Elektronid 1 ja 2 on juhtmest võrdsel kaugusel ning samuti ka elektronid 3 ja 4. Reasta elektronid vastavalt voolu

i

poolt tekitatud magnetjõudude suurustele, alates suurimast.

Answer

Joonisel 29-28 on näidatud kolm vooluringi, iga vooluring koosneb kahest radiaalsest sirglõigust ja kahest ringikaarest, millest ühe raadius on

r

ja teise raadius on

R > r

. Vooluringe läbivad võrdsed voolud ja nurk kahe radiaalse lõigu vahel vooluringides on võrdne. Reasta vooluringid vastavalt summaarse magnetvälja suuruse järgi keskmes, alustades suurimast.

Answer

Joonisel 29-29 on toodud neli asetust, milles pikkades paralleelsetes ja üksteisest võrdsetel kaugustel asuvates juhtmetes on võrdsed voolud suunaga risti lehekülje tasandiga. Reasta need asetused vastavalt voolude poolt keskmisele juhtmele rakendatud resultantjõu suurusele, alates suurimast.

Answer

Joonisel 29-30 on näidatud kolme pika sirge juhtme kolm võimalikku asetust; juhtmeid läbib võrdne vool kas siis otse lehekülje tasandi sisse või sellest välja. (a) Reasta need asetused vastavalt teiste juhtmete poolt juhtmele

A

rakendatud resultantjõu suuruse järgi, alustades suurimast. (b) Kas asetuse 3 puhul on nurk juhtmele

A

mõjuva resultantjõu ja punktiirjoone vahel võrdne, väiksem või suurem kui

45^{\circ}

Answer

Joonisel 29-31 on näidatud neli identset voolu

i

ja viis Ampère’i silmust (

a

kuni

e

), mis neid ümbritsevad. Reasta need silmused vastavalt integraali

\oint \to B \cdot d \to s

väärtusele joonisel näidatud suundades, alustades kõige positiivsemast.

Answer

Joonisel 9-32 on näidatud neli ringjoonelist Ampère’i silmust (

a

b

c

d

), mis asetsevad kontsentriliselt ümber juhtme, mille vool on suunatud lehekülje tasandist välja. Vool on ühtlane üle kogu juhtme ringikujulise ristlõike (toonitud ala joonisel). Reasta need silmused vastavalt

\oint \to B \cdot d \to s

väärtusele iga juhtme ümber, alustades suurimast.

Answer

Joonisel 29-33 on toodud radiaalse kauguse

r

funktsioonina magnetvälja suurus

B

nii sees- kui väljaspool nelja juhet (

a

b

c

d

), millest igaüks kannab voolu, mis on juhtme ristlõike ulatuses ühtlaselt jaotatud. Graafikute kattuvad osad on kahekordselt tähistatud. Reasta juhtmed vastavalt (a) raadiustele, (b) magnetvälja suurustele pinnal ning (c) voolu väärtustele, alustades suurimast. (d) Kas voolutiheduse suurus juhtmes a on suurem, väiksem või võrdne voolutiheduse suurusega juhtmes

c

Answer

Joonisel 29-34 on näidatud neli ringjoonelist Ampère’i silmust (

a

b

c

d

) ja ristlõikes neli pikka ringikujulise ristlõikega juhti (toonitud piirkonnad). Kolm neist juhtidest on seest õõnsad silindrid ning keskmine juht on täissilinder. Voolud juhtides, alustades vähimast raadiusest kuni suurima raadiuseni, on vastavalt

4 A

lehekülje tasandist välja,

9 A

lehekülje tasandisse,

5 A

lehekülje tasandist välja ning

3 A

lehekülje tasandisse. Reasta need Ampère’i silmused vastavalt integraal

\oint \to B \cdot d \to s

väärtusele, alustades suurimast.

Answer

Ülesanded

Punkt 29-2 Elektrivoolu magnetvälja arvutamine Punkt 29-3 Jõud kahe paralleelse voolu vahel Punkt 29-4 Ampère’i seadus Punkt 29-5 Solenoidid ja toroidid Punkt 29-6 Vooluga pool kui magnetiline dipool Supplementary exercises